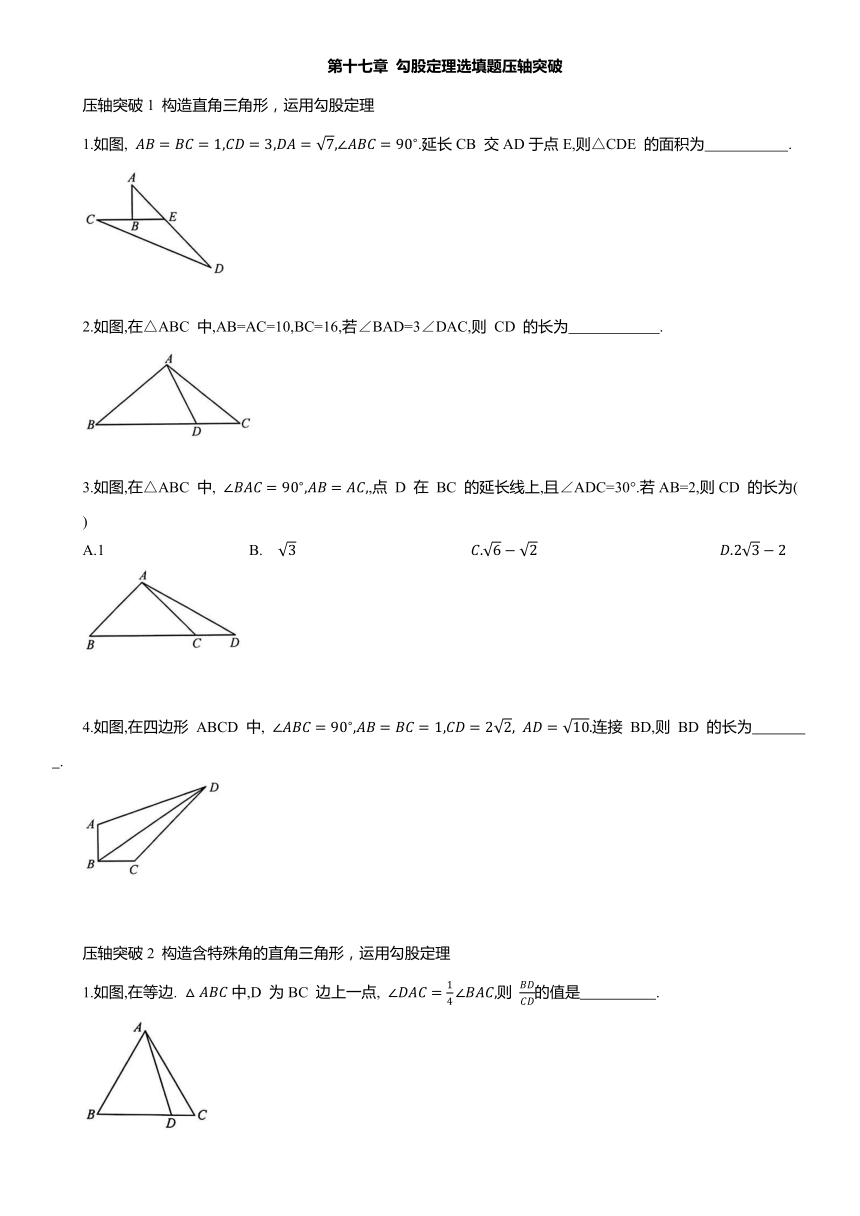
第十七章 勾股定理选填题压轴突破 （含详解）2024-2025学年人教版八年级数学下册

第十七章 勾股定理选填题压轴突破 压轴突破1 构造直角三角形，运用勾股定理 1.如图, .延长CB 交AD于点E,则△CDE 的面积为 . 2.如图,在△ABC 中,AB=AC=10,BC=16,若∠BAD=3∠DAC,则 CD 的长为 . 3.如图,在△ABC 中, ,点 D 在 BC 的延长线上,且∠ADC=30°.若AB=2,则CD 的长为( ) A.1 B. 4.如图,在四边形 ABCD 中, 连接 BD,则 BD 的长为 . 压轴突破2 构造含特殊角的直角三角形，运用勾股定理 1.如图,在等边. 中,D 为BC 边上一点, 则 的值是 . 2.如图,在等腰直角△OAB 中,∠AOB=90°,OA=OB=2,将OB绕点O 逆时针旋转30°得到OC,过点C 作CD∥OA 交AB 于点D,则CD 的长是( ) 3.如图,在△ABC 中,D 为边AC 的中点,E 为AB 上一点,若∠AED=150°,∠ABC=120°,则 的值为 . 4.如图,在 中， ,点 D 在BC 边上, 若 BC=10,则AD 的长为 . 压轴突破3 构造简单全等，运用勾股定理 1.如图,在四边形 ABCD 中, E 为线段CD 的中点,AD=1,CB=2,AE=3,则. 2.如图,在四边形 ABCD 中, 若 10 cm,则四边形ABCD 的面积为 3如图,在 Rt△ABC 中, ,D,E为BC上两点,若∠DAE=45°,∠ADE=60°,则 的值为 . 压轴突破4 折叠求线段的长或取值范围 1.如图,在矩形 ABCD 中,E 是 BC 的中点,将△ABE 折叠后得到△AFE,点 F 在矩形内部,延长AF 交CD 于点 H,若 则折痕 AE 的长为( ) C.3 2如图,在Rt△ABC中,∠ACB=90°,AC=1,BC=2,D 是边AB 上一点.连接CD,将△ACD 沿直线CD 折叠,点 A 落在点E 处,当点 E 在△ABC 的内部(不含边界)时，AD 长度的取值范围是 . 3.如图,在Rt△ABC 中,∠ACB=90°,AC=6,BC=8,D 是斜边AB 上一点.连接CD,将△ACD 沿直线CD 折叠,点 A 落在点E 处,当点 E 在△ABC 的内部(不含边界)时，AD长度的取值范围是 . 压轴突破5将军饮马型最值 1.如图,在矩形 ABCD 中, ,DE 平分 ,点 P 在DE 上,则AP+PB 的最小值是 . 2.如图,在正方形ABCD 中,点E,F 将对角线AC 三等分,且. 点 P 在正方形的边上，则满足 的点 P 的个数是( ) A.2 B.4 C.6 D.8 3.如图, ,M,N 分别在OA,OB 上,且( 4,点 P,Q 分别在OB,OA 上,则. 的最小值是 . 4.如图,在矩形ABCD 中, ,E、F 分别是AB 和DC 上的两个动点，M为 BC 的中点，则 的最小值是 ；若 则 EF+FM 的最小值为 . 压轴突破6 构造全等求最值 1.如图,在四边形 ABCD 中, 45°,则 BD 的最大值为 . 2.正方形 ABCD 的边长为10,E 是正方形外一动点, P 为AB 的中点.当点 E 运动时，线段 PE 的取值范围为 . E 3.如图,在 中， P 是 内一点，若AP+BP+CP 的最小值为 ,则BC 的长度为 . B 4.如图，在 中， O是 内一点，则点O到 三个顶点的距离之和的最小值是 . 压轴突破7 勾股定理与全等构造 1.如图,在 中， ,分别以CD,DE 为边在 外部作正方形 ABCD 和正方形 DEFG,若 则 2.如图,在四边形 ABCD 中, 若 则 BD 的长为( ) A.5 C.6 3.如图,在四边形ABCD中, 5,AD=7,则 BC 的长为 ,AC 的长为 . 4.在四边形 ABCD 中, ，若BC=5,DC=3,则AC的长为 . 5.如图,在等腰直角△CAB 中,CA=CB,点M,N 在直线AB 上,且∠MCN=135°,BM=8,AN=10,则MN 的长为 . 6.如图,在等腰直角△ACB 中,CA=CB,∠ACB=90°,∠ECF=45°,点 E,F 在AB 上,AM⊥AB,BN⊥AB,AM,BN分别交直线CE,CF 于点 M,N,若AM=2,BN=5,则 MN 的长为 . 7.如图,在四边形 ABCD 中,∠B=∠C=90°,E 为边BC 上一点,连接AE,DE,△ADE 是等边三角形,若 则 的值为 . 8.如图,在△ABC 中,∠B=45°,点 D 在BC 上,CE⊥AD 于点E,交AB 于点F,FC=AD,若AF=6,BC=8,则AC 的长是( ) A.5 -1 B.5 C.3 第十七章 勾股定理 压轴突破1 构造直角三角形，运用勾股定理 解:连接AC,∵∠ABC=90°,AB=BC=1, ∴△ACD 是直角三角形,∠CAD=90°, 2.5 解:过点 A 作AE⊥BC于点E,过点 D 作DF⊥AC 于点F, ∵AB=AC=10,BC=16,∴CE=8, 设∠CAD=x,则∠BAD=3x, ∵AE⊥BC,AB=AC,∴∠ ... ...