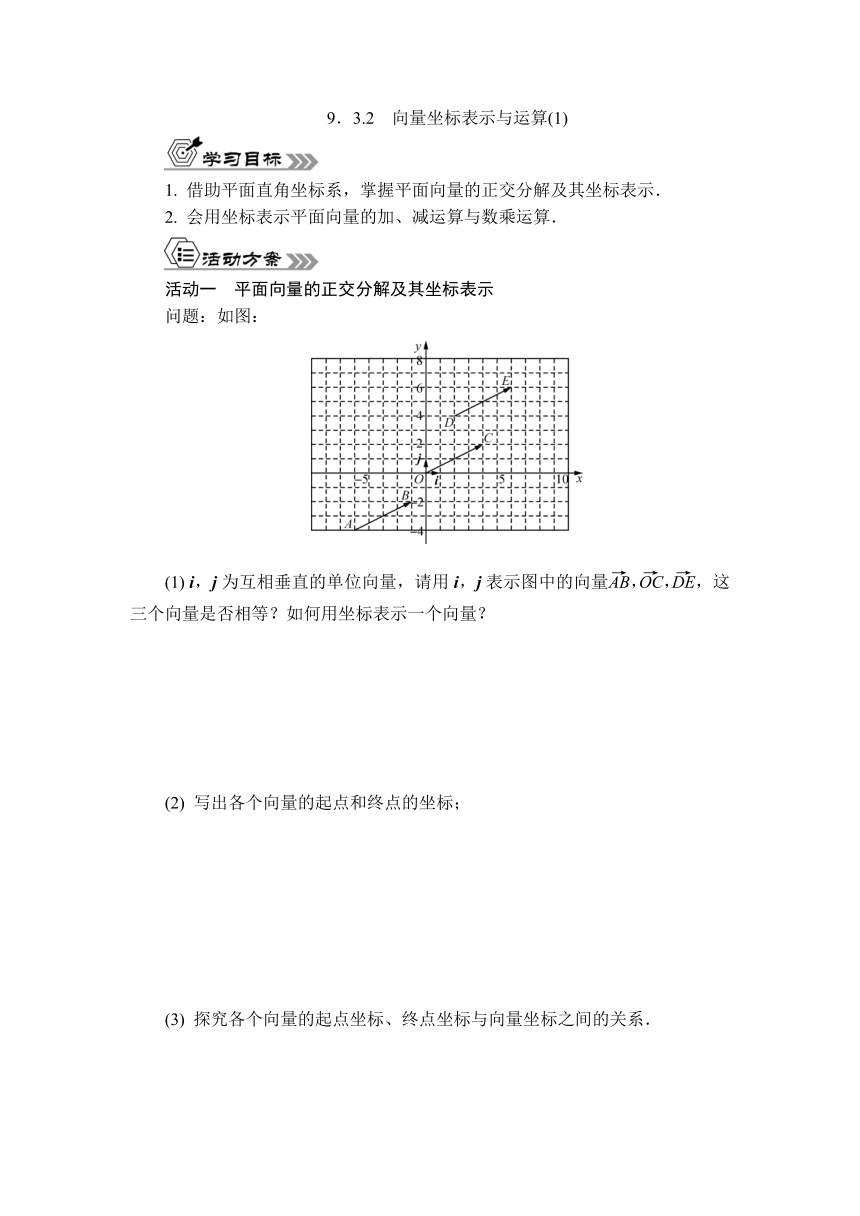
9.3.2 向量坐标表示与运算(1) 1. 借助平面直角坐标系,掌握平面向量的正交分解及其坐标表示. 2. 会用坐标表示平面向量的加、减运算与数乘运算. 活动一 平面向量的正交分解及其坐标表示 问题:如图: (1) i,j为互相垂直的单位向量,请用i,j表示图中的向量,,,这三个向量是否相等?如何用坐标表示一个向量? (2) 写出各个向量的起点和终点的坐标; (3) 探究各个向量的起点坐标、终点坐标与向量坐标之间的关系. 例1 如图,已知O是坐标原点,点A在第一象限,||=4,∠xOA=60°,求向量的坐标. 从原点引出的向量的坐标(x,y)就是点M的坐标. 如图,取与x轴,y轴相同方向的两个单位向量i,j作为基底,分别用i,j表示,,,并求出它们的坐标. 活动二 平面向量线性运算的坐标表示 1. 平面向量的坐标运算. 根据平面向量坐标表示的几何意义及向量的运算性质思考下列问题: 思考1 已知a=(x1,y1),b=(x2,y2),求a+b,a-b. 思考2 已知a=(x,y)和实数λ,求λa. 2. 平面向量坐标运算的应用. 例2 在平面直角坐标系中,O为坐标原点,已知点A(-1,3),B(1,-3),C(4,1),D(3,4),求向量,,,的坐标. 思考3 例2中的四边形OCDA是平行四边形吗?为什么? 一个向量的坐标等于该向量终点的坐标减去起点的坐标. 已知a=(3,4),b=(-1,4),求a+b,a-b,2a-3b的坐标. 已知a=(10,-4),b=(3,1),c=(-2,3),试用b,c表示a. 1. (教材改编)已知O为坐标原点,若向量=(3,2),=(-4,5),则点A的坐标为( ) A. (-1,7) B. (7,-3) C. (-1,-3) D. (7,7) 2. (2024成都期中)已知点O(0,0),向量=(2,3),=(6,-3),P是线段AB上靠近点A的三等分点,则点P的坐标为( ) A. B. C. D. 3. (多选)(2024张家口期中)已知平行四边形的三个顶点的坐标分别为(2,2),(-2,4),(0,0),则另一个顶点的坐标可以是( ) A. (0,-6) B. (0,6) C. (4,-2) D. (-4,2) 4. (2024北京期中)已知O为坐标原点,点A(3,-6),B(-5,2),=(+),则点C的坐标为_____. 5. 已知a=(2,-4),b=(-1,3),c=(6,5),p=a+2b-c,试用a,b表示p. 9.3.2 向量坐标表示与运算(2) 1. 能用坐标表示平面向量的数量积及夹角. 2. 能用坐标表示平面向量垂直的条件. 活动一 掌握平面向量数量积的坐标表示 1. 两个非零平面向量垂直的等价条件: 2. 设i,j分别是与x轴,y轴正方向相同的两个单位向量,则i·i=_____,j·j=_____,i·j=j·i=_____. 3. 探究:若两个向量a=(x1,y1),b=(x2,y2),i,j分别是与x轴,y轴正方向相同的单位向量. (1) 将a,b用向量i和j表示; (2) 根据向量数量积的定义及上面的结论计算a·b; (3) 由(1)(2)得出用a,b的坐标来表示它们的数量积a·b. 4. 平面向量数量积的坐标表示. (1) 平面向量数量积的坐标表示: 根据上述探究,如果两个向量a=(x1,y1),b=(x2,y2),那么平面两向量数量积的坐标表示为: 特别地,设a=(x,y),则a·a的几何意义是什么?你能得到什么结论?(|a|2=?即|a|=?) (2) 平面内两点间的距离公式: ①已知两点A(x1,y1),B(x2,y2),求; ②能否用(1)的结论求|| ③||的几何意义是什么? 根据①②③得出A(x1,y1),B(x2,y2)两点间的距离公式为: (3) 两向量夹角的余弦(0≤θ≤π): ①设两个非零向量a=(x1,y1),b=(x2,y2),它们的夹角是θ,根据向量数量积的定义,如何用向量a和b的坐标来表示它们夹角的余弦? ②特别地,若a⊥b,则向量a和b的坐标满足什么条件? ③反之,向量a和b的坐标满足上述条件,则a⊥b成立吗? 由此得出:a⊥b a·b=0 _____. 活动二 掌握平面向量数量积的坐标表示的应用 例1 已知△ABC的三个顶点坐标分别为A(1,2),B(2,3), ... ...
~~ 您好,已阅读到文档的结尾了 ~~