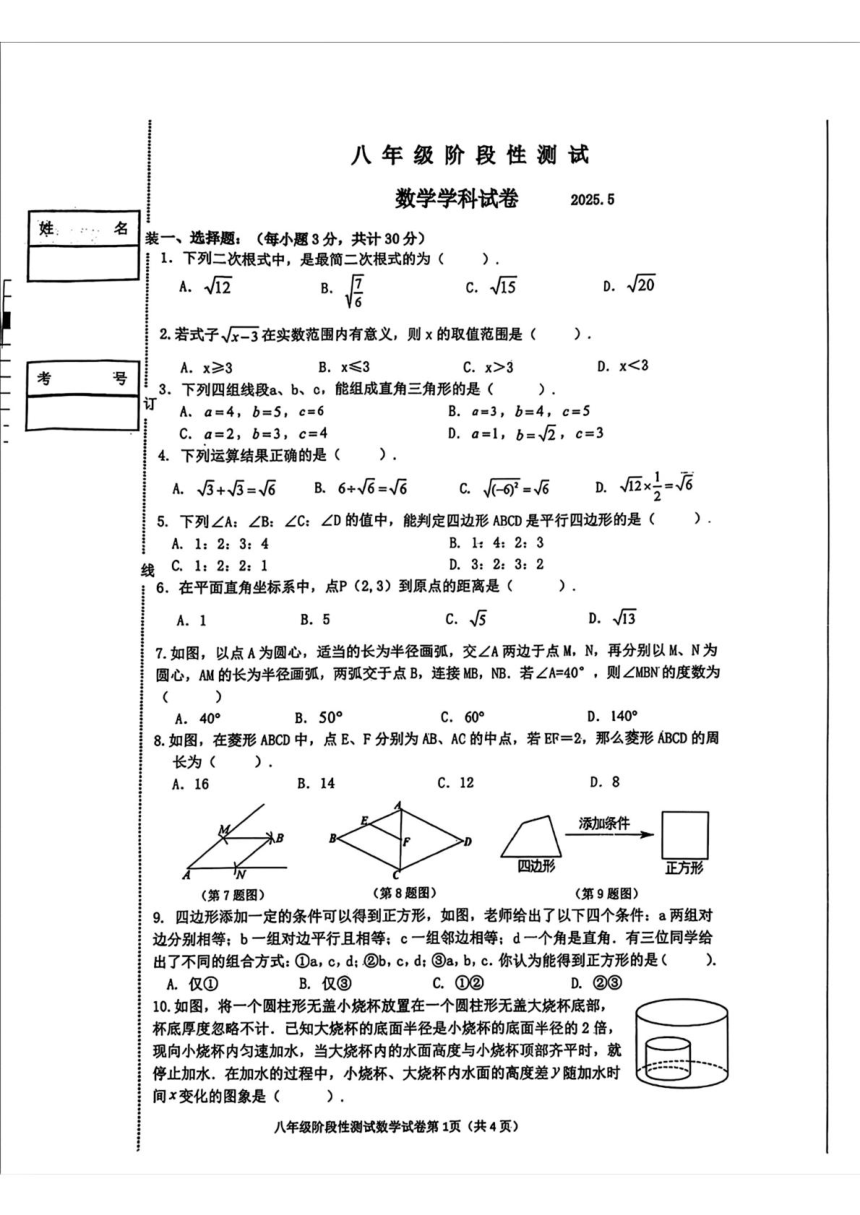
八年级阶段性测试 数学学科试卷 2025.5 姓 否 装一、选择题:(每小题3分,共计30分) 1. 下列二次根式中,是最简二次根式的为( A.2 B. 居 c.5 D.V20 2.若式子√-3在实数范围内有意义,则x的取值范围是( 考 号 A.x≥3 B.x≤3 C.x>3 D.x<3 .下列四组线段a、b、c,能组成直角三角形的是( ) 订 A.a=4,b=5,c=6 B.a=3,b=4,c=5 C.a=2,b=3,c=4 D.a=1,b=√5,c=3 4.下列运算结果正确的是( A.5+5=√6 B.6+V6=√6 C.= D.2x1=6 5.下列∠A:∠B:∠C:∠D的值中,能判定四边形ABCD是平行四边形的是( A.1:2:3:4 B.1:4:2:3 线C.1:2:2:1 D.3:2:3:2 6.在平面直角坐标系中,点P(2,3)到原点的距离是( ) A.1 B.5 c.5 D.√3 7.如图,以点A为圆心,适当的长为半径画弧,交∠A两边于点M,N,再分别以M、N为 圆心,AW的长为半径画弧,两弧交于点B,连接MB,NB.若∠A=40°,则∠MBN的度数为 () A.40° B.50° C.60° D.140° 8.如图,在菱形ABCD中,点E、F分别为B、AC的中点,若EF=2,那么菱形ABCD的周 长为( ). A.16 B.14 C.12 D.8 添动条件 四边形 正方形 (第7题图) (第8题图) (第9题图) 9. 四边形添加一定的条件可以得到正方形,如图,老师给出了以下四个条件:a两组对 边分别相等:b一组对边平行且相等:c一组邻边相等:d一个角是直角.有三位同学给 出了不同的组合方式:①a,c,d:②b,c,d:③a,b,c.你认为能得到正方形的是( A.仅① B.仅③ C.①② D.②③ 10.如图,将一个圆柱形无盖小烧杯放置在一个圆柱形无盖大烧杯底部, 杯底厚度忽略不计.已知大烧杯的底面半径是小烧杯的底面半径的2倍, 现向小烧杯内匀速加水,当大烧杯内的水面高度与小烧杯顶部齐平时,就 停止加水.在加水的过程中,小烧杯、大烧杯内水面的高度差y随加水时 间x变化的图象是( 八年级阶段性测试数学试卷第1页(共4页) 二、填空题: (每小题3分,共30分) 11.计算:4÷V2= 12.菱形ABCD中,若对角线AC=2互,BD=√5,则菱形ABCD的面积为 13.在如图所示的图形中,所有四边形都是正方形,所有三角形都是直角三角形,若正方形A、C、D的 面积依次为5、6、20,则正方形B的面积是 14.如图,m/1m,点C、D、E在直线m上,四边形ABED为平行四边形,若△ABC的面积为3,则平行 四边形ABED的面积是 B (第13题图) (第14题图) (第15题图) 15.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等 的直角三角形,得到一个恒等式.后人惜助这种分割方法所得的图形证明了勾股定理,如图所示的就 用了这种分割方法,若BC-4,AE=2,则正方形DECF的边长等于 16.我们规定:对于任意的正数m,r的“※”运算为,m※n=2√面-√石,升算8※18的结果 为 17.如图,点E是矩形ABCD的对角线AC的延长线上一点,若AC-2BE,∠ACB=65°,则∠E= 18.如图,在菱形ABCD中,∠A=60°,8=2,动点E、F分别在线段AB、BC上,且BE=CF,则EF 的最小值为 B (第17题图) (第18题图) (第20题图) 19.在平行四边形ABCD中,∠ABC=30°,AB=4,对角线AC√7,则平行四边形ABCD的面积为 20.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB,交CB的延 长线于G,连接GP,AD⊥BD.下列结论:①DE∥BF:②四边形BEDF是菱形:⑨S平行图边形An=4S△: ④若AB=6,AD=4,那么FG=,√55,其中所有正确结论的序号是 三解答题(其中21~22题各7分,23~24题各8分:25~27题各10分,共计60分) 21.计算(本题7分) ①22-6E+34 (2)(√5+5)(5-5) 八年级阶段性测试数学试卷第2页(共4页) ... ...
~~ 您好,已阅读到文档的结尾了 ~~