第二十二章 二次函数 解答题训练 （含简单答案）人教版九年级上册数学

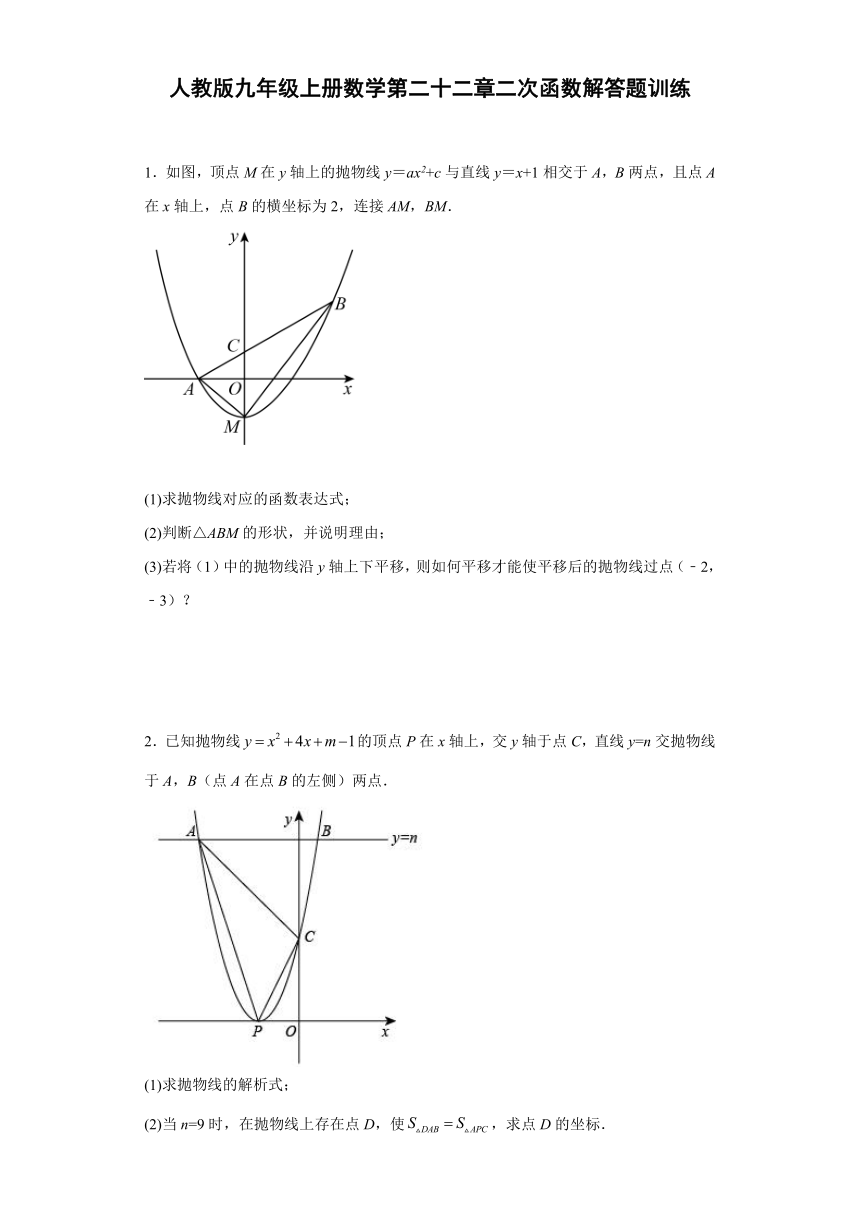
人教版九年级上册数学第二十二章二次函数解答题训练 1．如图，顶点M在y轴上的抛物线y＝ax2+c与直线y＝x+1相交于A，B两点，且点A在x轴上，点B的横坐标为2，连接AM，BM． (1)求抛物线对应的函数表达式； (2)判断△ABM的形状，并说明理由； (3)若将（1）中的抛物线沿y轴上下平移，则如何平移才能使平移后的抛物线过点（﹣2，﹣3）？ 2．已知抛物线的顶点P在x轴上，交y轴于点C，直线y=n交抛物线于A，B（点A在点B的左侧）两点． (1)求抛物线的解析式； (2)当n=9时，在抛物线上存在点D，使，求点D的坐标． 3．如图，抛物线y＝﹣x2＋bx＋c的对称轴为直线x＝，其图象与直线y＝x＋2交于C，D两点，其中点C在y轴上，点P是y轴右侧的抛物线上一动点，过点P作PE⊥x轴于点E，交CD于点F． (1)求抛物线的解析式； (2)若点P的横坐标为x0，当x0为何值时，以O，C，P，F为顶点的四边形是平行四边形？请说明理由． 4．如图，在平面直角坐标系中，抛物线分别交轴，轴于点A，和点，抛物线与抛物线关于直线对称，两条抛物线的交点为，（点在点的左侧）． (1)求抛物线的表达式； (2)将抛物线沿轴正方向平移，使点与点重合，求平移的距离； (3)在（2）的条件下：规定抛物线和抛物线在直线下方的图象所组成的图象为，点，和，在函数上（点在点的右侧），在（2）的条件下，若，且，求点坐标． 5．如图，抛物线y＝ax2+bx+c经过点A（﹣2，5），与x轴相交于B（﹣1，0），C（3，0）两点． (1)求抛物线的函数表达式； (2)点D在抛物线的对称轴上，且位于x轴的上方，将△BCD沿直线BD翻折得到△BC'D，若点C'恰好落在抛物线的对称轴上，求点C'和点D的坐标； (3)设P是抛物线上位于对称轴右侧的一点，点Q在抛物线的对称轴上，当△CPQ为等边三角形时，求直线BP的函数表达式． 6．如图，在平面直角坐标系中，已知抛物线L：与x轴相交于A，B两点，与一次函数相交于点A和点C． (1)求点A、B、C三点的坐标； (2)点P是抛物线上的一动点且在直线AC的上方，过点P作x轴垂线交直线AC于点D，当点P运动到什么位置时，线段PD的长度最大？求出此时点P的坐标和线段PD的最大值； (3)将抛物线L：的图像向下平移得到新的抛物线，直线AC与抛物线交于M，N两点，满足，在抛物线上有且仅有三个点，，使得△，△，的面积均为定值S，求出定值S及，，的坐标． 7．二次函数的部分图象如图所示，对称轴是直线x＝﹣1． (1)求这个二次函数的解析式； (2)求该图象的顶点坐标； (3)观察图象，当y＞0时，求自变量x的取值范围． 8．已知，如图抛物线与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为，． (1)求抛物线的解析式； (2)若点D是线段AC下方抛物线上的动点，求四边形AOCD面积的最大值； (3)若点E在x轴上，点P在抛物线上．是否存在以A，C，E，P为顶点且以AC为一边的平行四边形？若存在，请直接写出点P的坐标；若不存在，请说明理由． 9．已知二次函数y＝ax2+bx+3的图像和x轴交于点A（﹣3，0）、B（1，0），与y轴交于点C、D（0，﹣1）． (1)求二次函数解析式； (2)在线段AC上方的抛物线上有一动点P，直线PC与直线BD交于点Q，当△PAQ面积最大时，求点P的坐标及△PAQ面积的最大值； (3)在（2）条件下，将抛物线y＝ax2+bx+3沿射线AC平移2个单位长度，得到新二次函数y′＝ax2+bx+c，点R在新抛物线对称轴上，在直线y＝﹣x上有一点S，使得以点P，D，R，S为顶点的四边形是平行四边形，写出所有符合条件的点R的坐标，并写出求解点R的坐标的其中一种情况的过程． 10．如图，抛物线（a≠0）与直线y=x+1相交于A（-1，0），B（4，n）两点，且抛物线经过点C（5，0）． (1)求抛物线的解析式； (2)点P是直线AB上方抛物线上的一个动点（不与点A、点B重合），过点P作直线PD⊥x轴于点D，交直线AB于点E，设点 ... ...