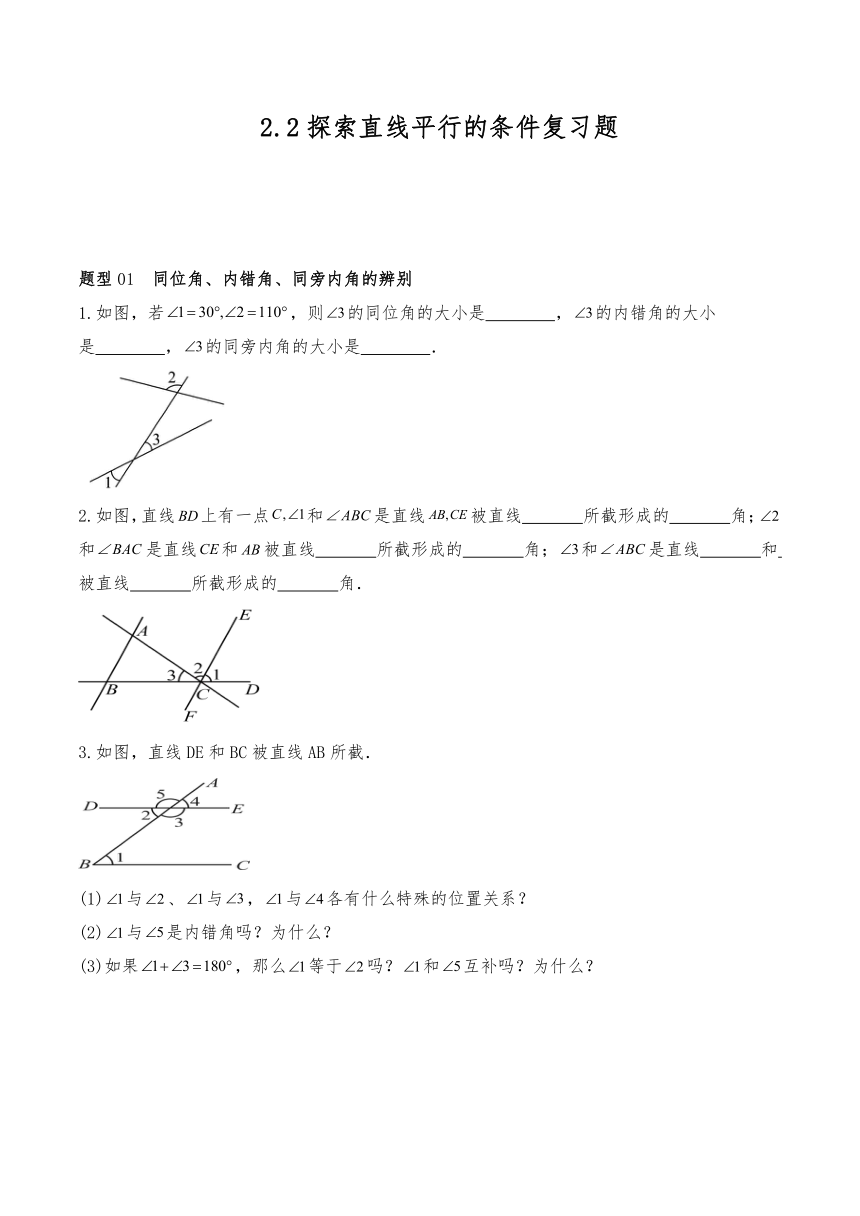
2.2探索直线平行的条件复习题 题型01 同位角、内错角、同旁内角的辨别 1.如图,若,则的同位角的大小是 ,的内错角的大小是 ,的同旁内角的大小是 . 2.如图,直线上有一点和是直线被直线 所截形成的 角;和是直线和被直线 所截形成的 角;和是直线 和 被直线 所截形成的 角. 3.如图,直线DE和BC被直线AB所截. (1)与、与,与各有什么特殊的位置关系? (2)与是内错角吗?为什么? (3)如果,那么等于吗?和互补吗?为什么? 题型02 平面内两直线的位置关系 1.同一平面内,两条不重合的直线的位置关系是( ) A.平行 B.相交 C.相交或平行 D.垂直 2.在同一平面内有三条不同的直线,若,则a与b的位置关系为( ) A.相交但不垂直 B.垂直 C.平行 D.无法确定 3.、、为同一平面内的三条直线,若与不平行,与不平行,那么与( ) A.一定不平行 B.一定平行 C.一定互相垂直 D.可能相交或平行 题型03 平行公理及推论应用 1.平行线的基本事实:过 与这条直线平行. 2.有下列说法:①两条不相交的直线是平行线;②过一点有且只有一条直线与已知直线平行;③在同一平面内,和第三条直线都不相交的两条直线平行;④在同一平面内,不相交的两条射线必平行.其中,正确的有 个. 3.下列说法:①在同一平面内,若直线,,则;②在同一平面内,若直线,直线与相交,则直线与相交;③若直线与直线相交,直线与直线相交,则直线与直线相交;④过一点有且只有一条直线与已知直线平行,其中说法正确的是 .(填序号) 题型04 同位角相等,两直线平行 1.把下面的证明过程补充完整: 如图,已知直线,被直线所截,为与的交点,于点,,,求证:. 证明:∵(已知), ∴( ). 又∵(已知), ∴, ∴( )(_____). 又∵(已知), ∴, ∴(_____). 2.如图:,平分,平分,,试说明:.请完成下面的解题过程. 解:∵平分,平分(已知), _____,_____(角平分线的定义), 又(已知) _____. 又(已知) _____, (_____). 3.如图,在三角形中,,点分别在边的延长线上,作射线,如果平分,那么与平行吗?为什么? 题型05 内错角相等,两直线平行 1.完成下面证明: 如图,平分,.求证. 证明:∵平分 ∴( ) ∵. ∴ .( ) ∴( ). 2.如图,点G在上,已知,平分,平分,请说明的理由. 解:(已知), (_____) (_____). ∵平分, _____(_____). 平分, _____, 得(_____), (_____). 3.如图,点O在直线上,平分平分是上一点,连接. (1)判断与是否垂直,并说明理由; (2)若与互余,判断与是否平行,并说明理由. 题型06 同旁内角互补,两直线平行 1.如图,已知.将下列推理过程补充 完整. ∵(已知), ∴_____(_____) ∵(已知) ∴_____(_____) ∵(已知), ∴_____(_____). 2.完成下面的证明. 已知:如图,. 求证:. 证明:, _____(_____). , _____. (_____). 3.完成下面的证明: 如图,平分,平分,且,求证. 证明:∵平分(已知), ∴( ) ∵平分(已知), ∴_____( ) ∴( ) ∵(已知), ∴_____( ) ∴( ) 题型07 添加一条件使两直线平行 1.如图,已知,点,分别在射线,上,点为内一点,连接,,不添加辅助线,请添加一个条件使得,则可添加为 .(写出一个即可) 2.如图,E是线段的延长线上一点,添加一个条件,使,则可添加的条件为 (写出一种情况即可). 3. 如图,已知,请你添加一个条件,使得能利用“内错角相等,两直线平行”来判断,你添加的条件是 . 题型08 垂直于同一条直线的两条直线平行 1.如图,已知,,试探究与的位置关系,并说明理由. 2.如图,,,垂足分别是,,. (1)判断与的位置关系;(不需要证明) (2)求证:. 题型09 平行线的判定去判 ... ...
~~ 您好,已阅读到文档的结尾了 ~~