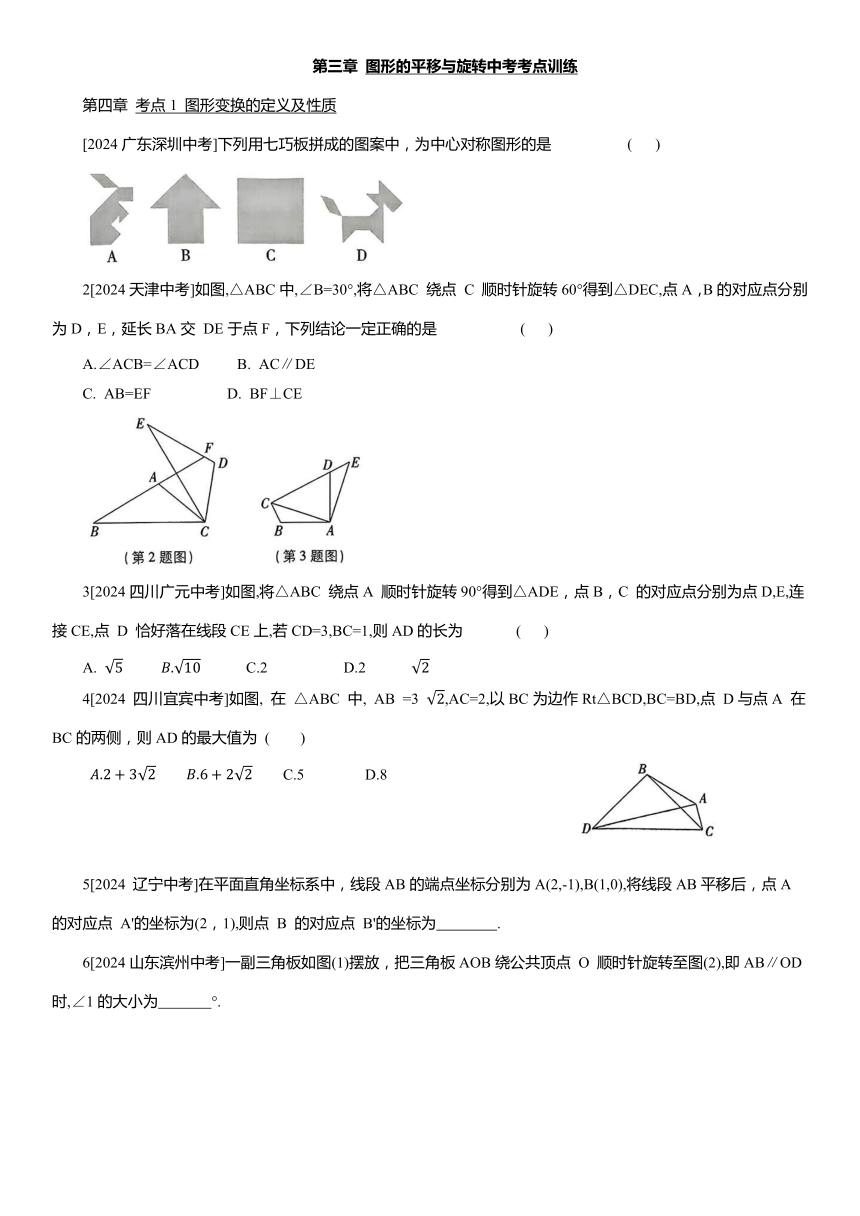
图形的平移与旋转中考考点训练 考点1 图形变换的定义及性质 [2024广东深圳中考]下列用七巧板拼成的图案中,为中心对称图形的是 ( ) 2[2024天津中考]如图,△ABC中,∠B=30°,将△ABC 绕点 C 顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交 DE于点F,下列结论一定正确的是 ( ) A.∠ACB=∠ACD B. AC∥DE C. AB=EF D. BF⊥CE 3[2024四川广元中考]如图,将△ABC 绕点A 顺时针旋转90°得到△ADE,点B,C 的对应点分别为点D,E,连接CE,点 D 恰好落在线段CE上,若CD=3,BC=1,则AD的长为 ( ) A. C.2 D.2 4[2024 四川宜宾中考]如图, 在 △ABC 中, AB =3 ,AC=2,以BC为边作Rt△BCD,BC=BD,点 D与点A 在BC的两侧,则AD的最大值为 ( ) C.5 D.8 5[2024 辽宁中考]在平面直角坐标系中,线段AB的端点坐标分别为A(2,-1),B(1,0),将线段AB平移后,点A 的对应点 A'的坐标为(2,1),则点 B 的对应点 B'的坐标为 . 6[2024山东滨州中考]一副三角板如图(1)摆放,把三角板AOB绕公共顶点 O 顺时针旋转至图(2),即AB∥OD时,∠1的大小为 °. 7[2024北京中考]已知 点B,C分别在射线AN,AM 上,将线段BC绕点B顺时针旋转180°-2α得到线段BD,过点D作AN的垂线交射线AM 于点 E. (1)如图(1),当点 D 在射线AN上时,求证:C是AE的中点; (2)如图(2),当点 D 在∠MAN内部时,作DF∥AN,交射线AM于点 F,用等式表示线段 EF 与AC 的数量关系,并证明. 8[2024 黑龙江牡丹江中考]数学老师在课堂上给出了一个问题,让同学们探究.在 Rt△ABC中,∠ACB=90°,∠BAC=30°,点 D 在直线 BC上,将线段AD 绕点A 顺时针旋转60°得到线段AE,过点 E作EF∥BC,交直线AB 于点 F. (1)当点 D 在线段 BC 上时,如图(1),求证:BD+EF=AB. 分析问题:某同学在思考这道题时,想利用AD=AE构造全等三角形,便尝试着在AB 上截取AM=EF,连接DM,通过证明两个三角形全等,最终证出结论. 推理证明:写出图(1)的证明过程. 探究问题: (2)当点D 在线段BC 的延长线上时,如图(2);当点 D 在线段 CB 的延长线上时,如图(3),请判断并直接写出线段 BD,EF,AB 之间的数量关系. 拓展思考: (3)在(1)(2)的条件下,若 2BD,则EF= . 考点2 图形变换的作图 [2023安徽中考]如图,在由边长为1个单位长度的小正方形组成的网格中,点A,B,C,D均为格点(网格线的交点). (1)画出线段 AB 关于直线 CD 对称的线段A B ; (2)将线段AB 向左平移2个单位长度,再向上平移1个单位长度,得到线段A B ,画出线段A B ; (3)描出线段AB上的点 M 及直线 CD 上的点N,使得直线MN垂直平分AB. 10[2024安徽中考]如图,在由边长为1个单位长度的小正方形组成的网格中建立平面直角坐标系xOy,格点(网格线的交点)A,B,C,D的坐标分别为(7,8),(2,8),(10,4),(5,4). (1)以点D 为旋转中心,将△ABC 旋转180°得到△A B C ,画出△A B C ; (2)直接写出以B,C ,B ,C为顶点的四边形的面积; (3)在所给的网格图中确定一个格点 E,使得射线AE平分∠BAC,写出点 E 的坐标. 1. C【解析】选项 A、B、D均不能找到这样的一个点,使图形绕该点旋转180度后和原图形完全重合,所以不是中心对称图形;选项C能找到这样的一个点,使图形绕该点旋转180度后和原图形完全重合,所以是中心对称图形.故选 C. 2. D 【解析】记 BF 与CE相交于点H,如图所示.∵将 绕点C顺时针旋转( 得到 ∵ ∠B=30°,∴ 在△BHC 中,∠BHC=180°-∠BCE-∠B=90°,∴BF⊥CE,故D 选项正确,符合题意.设∠ACH=x°, ∴∠ACB=60°-x°.∵ ∠B=30°,∴ ∠EDC=∠BAC= 180°-30°-(60°-x°) = 90°+x°, ∵x°不一定等于30°,∴ ∠EDC+∠ACD 不一定等于180°,∴AC∥DE 不一定成立,故B选项不正确,不符合题意.∵ ∠ACB=60°-x°,∠ACD=60°,x°不一定等于 0°,∴∠ACB =∠ACD 不一定成立,故A 选项不正确,不 ... ...
~~ 您好,已阅读到文档的结尾了 ~~