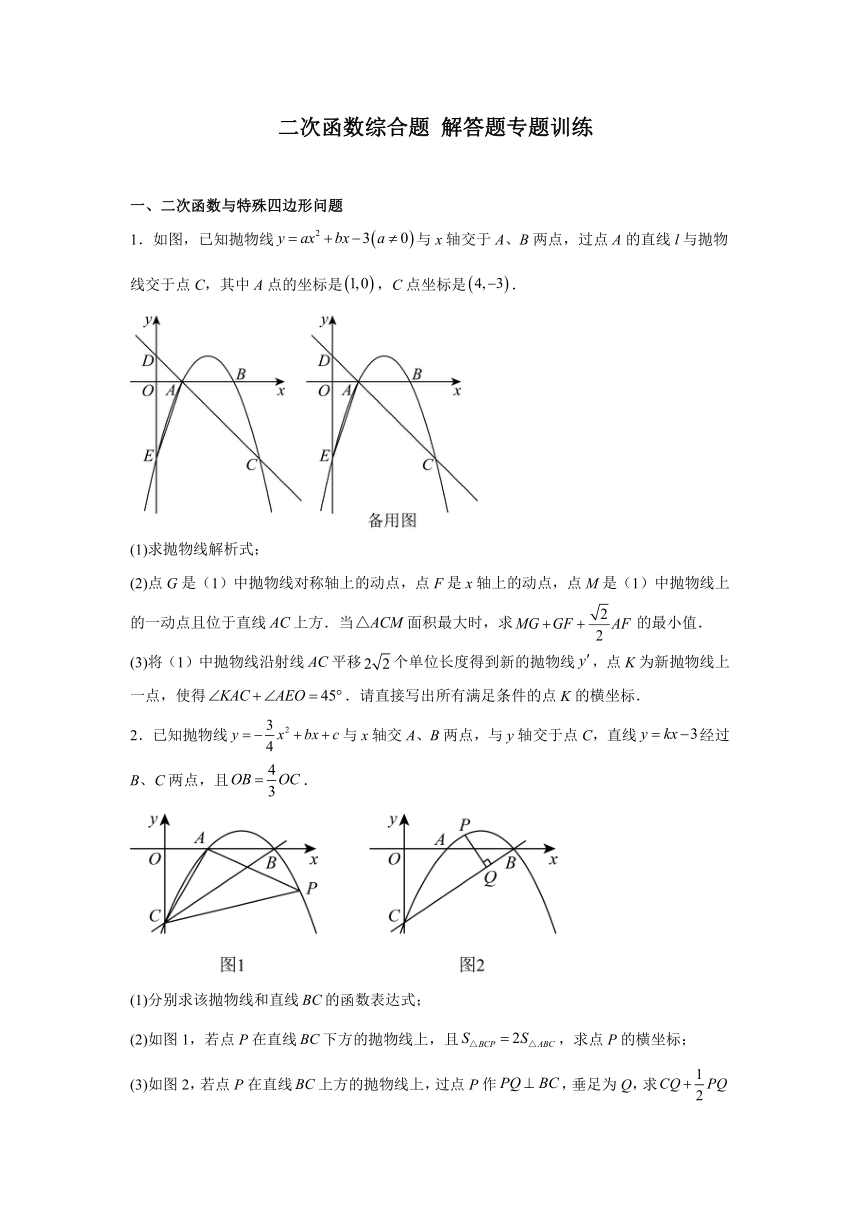
二次函数综合题 解答题专题训练 一、二次函数与特殊四边形问题 1.如图,已知抛物线与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是,C点坐标是. (1)求抛物线解析式; (2)点G是(1)中抛物线对称轴上的动点,点F是x轴上的动点,点M是(1)中抛物线上的一动点且位于直线上方.当面积最大时,求的最小值. (3)将(1)中抛物线沿射线平移个单位长度得到新的抛物线,点K为新抛物线上一点,使得.请直接写出所有满足条件的点K的横坐标. 2.已知抛物线与x轴交A、B两点,与y轴交于点C,直线经过B、C两点,且. (1)分别求该抛物线和直线的函数表达式; (2)如图1,若点P在直线下方的抛物线上,且,求点P的横坐标; (3)如图2,若点P在直线上方的抛物线上,过点P作,垂足为Q,求的最大值. 3.如图,已知抛物线经过点与点,且交轴于点. (1)求该抛物线的表达式,并写出其顶点坐标; (2)将该抛物线向上平移4个单位,再向右平移个单位,得到新抛物线.若新抛物线的顶点为,连结,直线将分割成面积相等的两个三角形. ①求的值; ②在新的抛物线上寻找点,使,求点的坐标. 4.如图,在平面直角坐标系中,抛物线与轴交于点,,其中点的坐标为,与轴交于点. (1)求抛物线和直线的函数表达式; (2)点是直线上方的抛物线上一个动点,当面积最大时,求点的坐标; (3)连接和(2)中求出的点、点位于直线下方且在抛物线上,若,求点的坐标. 5.如图,已知抛物线经过两点,与y轴交于C点. (1)求抛物线表达式; (2)点P是直线上方的抛物线上的一动点(不与B、C重合),是否存在点P,使的面积最大.若存在,请求出的最大面积,若不存在,试说明理由; (3)若点M在x轴上,点N在抛物线上,以A、C、M、N为顶点的四边形是平行四边形时,请直接写出点M点坐标. 二、二次函数与角度问题 6.如图,已知抛物线的图象与x轴交于点、,与y轴交于点C,且. (1)求该抛物线的表达式; (2)如图①,在直线上方的抛物线上存在一点M,使得,求出M的坐标; (3)若点P是该抛物线上位于直线下方的一动点,从点C沿抛物线向点A运动(点P与A不重合),点D在抛物线对称轴上,点Q是平面内任意一点,当B,P,D,Q四点构成的四边形为正方形时,请直接写出Q点的坐标. 7.综合与探究:如图1,在平面直角坐标系中,抛物线与x轴交于点和点,与y轴交于点,点是抛物线上点与点之间的动点(不包括点,点). (1)求抛物线的解析式; (2)如图1,动点P 在直线上方的抛物线上,求面积的最大值及此时点的坐标; (3)如图2,过原点0作直线I交抛物线于E、F两点,点E的横坐标为e,点F的横坐标为f,求证:是一个定值. 8.如图,已知抛物线与轴交于A、B两点,与轴交于C点,直线交抛物线于点D,并且,. (1)求抛物线的解析式; (2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形面积的最大值; 9.如图①,已知抛物线与轴交于,两点,与轴交于点. (1)求该抛物线的表达式; (2)若点是抛物线上第一象限内的一个动点,连接,,,.当的面积等于面积的2倍时,求点的坐标; (3)抛物线上是否存在点,使得?若存在,请直接写出点的坐标. 10.点 、、 的坐标为分别,抛物线经过这三点. (1)求抛物线的解析式; (2)若点,是抛物线上的两个动点,且点 在直线 下方. ①如图1,过 点作轴的垂线,垂足为,交直线 于点,连接,,,猜想与的数量关系,并说明理由; ②如图2,点 在直线 上,且横坐标为,过点 作轴于点 ,求线段 长度的最大值. 三、二次函数与特殊三角形问题 11.已知平面直角坐标系中,O为坐标原点,抛物线与x轴交于A,B两点,与y轴的正半轴交于C点,且; (1)求抛物线的解析式; (2)如图1,点P是抛物线在第一象限内的一点,连接,过点P作轴于点D,交 ... ...
~~ 您好,已阅读到文档的结尾了 ~~