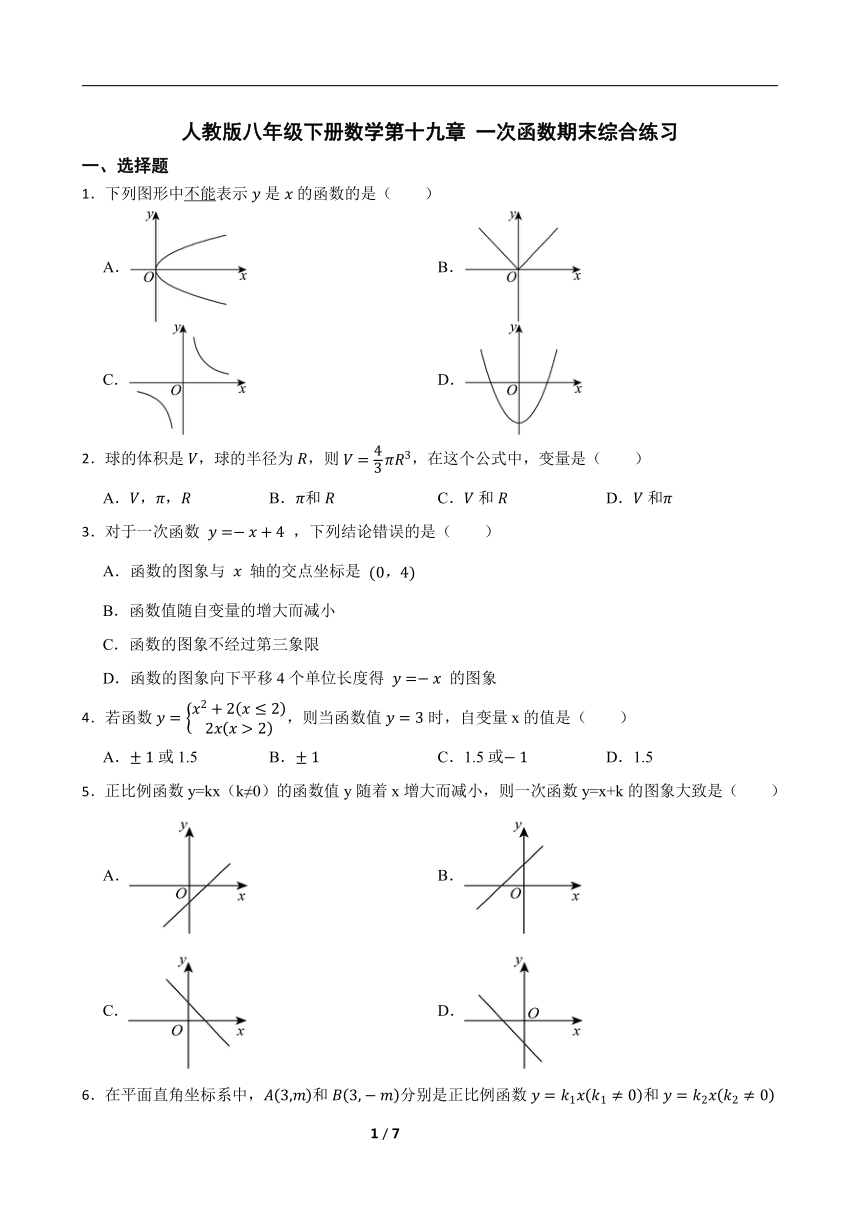
人教版八年级下册数学 第十九章 一次函数 期末综合练习（含答案）

人教版八年级下册数学第十九章 一次函数期末综合练习 一、选择题 1．下列图形中不能表示是的函数的是（　　） A． B． C． D． 2．球的体积是，球的半径为，则，在这个公式中，变量是（　　） A．，， B．和 C．和 D．和 3．对于一次函数 ，下列结论错误的是（　　） A．函数的图象与 轴的交点坐标是 B．函数值随自变量的增大而减小 C．函数的图象不经过第三象限 D．函数的图象向下平移4个单位长度得 的图象 4．若函数，则当函数值时，自变量x的值是（　　） A．或1.5 B． C．1.5或 D．1.5 5．正比例函数y=kx（k≠0）的函数值y随着x增大而减小，则一次函数y=x+k的图象大致是（　　） A． B． C． D． 6．在平面直角坐标系中，和分别是正比例函数和图象上的点，则，一定满足（　　） A． B． C． D． 7．已知正比例函数的图象上两点，，当时，，那么的取值范围是（　　） A． B． C． D． 8．已知方程 解是 ，则直线 与 的交点是（　　） A．（1，0） B．（1，3） C．（-1，-1） D．（-1，5） 9．如图，直线y=-2x+2与直线y=kx+b(k、b为常数，k≠0)相交于点A(-1，m)，则关于×的不等式-2x+2-1 B．x<-1 C．x≦-1 D．x≧-1 10．如图，已知点，，，，为直线上一动点，则的对角线的最小值是（　　） A． B．4 C．5 D． 二、填空题 11．一次函数的图像与y轴交于y轴正半轴，则m的取值范围是　（1） 　． 12．若是关于的一次函数，则的值为　 　． 13．若，两点都在一次函数的图象上，则　 　． 14．一种弹簧秤最大能称不超过的物体，不挂物体时弹簧的长为，每挂重物体，弹簧伸长，在弹性限度内，挂重后弹簧的长度y（）与所挂物体的质量x（）之间的函数关系式为　 　． 15．我们知道：当 时，不论 取何实数，函数 的值为3，所以直线 一定经过定点 ；同样，直线 一定经过的定点为　 　. 三、解答题 16．已知正比例函数y=kx． （1）若函数图象经过第二、四象限，则k的范围是什么？ （2）点（1，-2）在它的图象上，求它的表达式． 17．某乳品公司向某地运输一批牛奶，若由铁路运输只需每千克运费0.6元；若由公路运输，除了每千克运费0.3元外，还需额外费用600元. （1）设该公司运输的这批牛奶为xkg，选择铁路运输时，所需运费为y1元，选择公路运输时，所需运费为y2元，请分别写出y1、y2与x之间的关系式； （2）若公司只支出运费1500元，则选用哪种运输方式运送的牛奶多 若公司运送1500kg牛奶，则选用哪种运输方式所需用较少 18．如图，已知直线经过点，交y轴于点B，直线与直线交于点C，交y轴于点D． （1）求b的值； （2）求的面积； （3）当时，x的取值范围是 ．（直接写出结果） 19．如图，在平面直角坐标系中，直线交y轴于点，交x轴于点B，直线交x轴于点C，交y轴于点D，且，，． （1）求直线与直线的解析式； （2）点E为直线上一动点，若，求点E的坐标； （3）若点F是直线上一点，点G是x轴上一点，当与全等时，请直接写出点F的坐标． 20．已知甲加工A型零件60个所用时间和乙加工B型零件80个所用时间相同，甲、乙两人每天共加工35个零件，设甲每天加工x个A型零件． （1）求甲、乙每天各加工零件多少个？ （2）根据市场预测，加工A型零件所获得的利润为m元/件（3≤m≤5），加工B型零件所获得的利润每件比A型少1元．求甲、乙每天加工的零件所获得的总利润P（元）与m的函数关系式，并求P的最大值和最小值． 21．为保护学生视力，课桌椅的高度都是按一定的关系配套设计的，研究表明：假设课桌的高度为ycm，椅子的高度为xcm，则y应是x 的一次函数，下表列出两套符合条件的课桌椅的高度： 第一套 第二套 椅子高度xcm 40 37 桌子高度ycm 75 70 （1）请确定y与x的函数关系式； （2）现有一把高39cm的椅子和一张高为72. ... ...