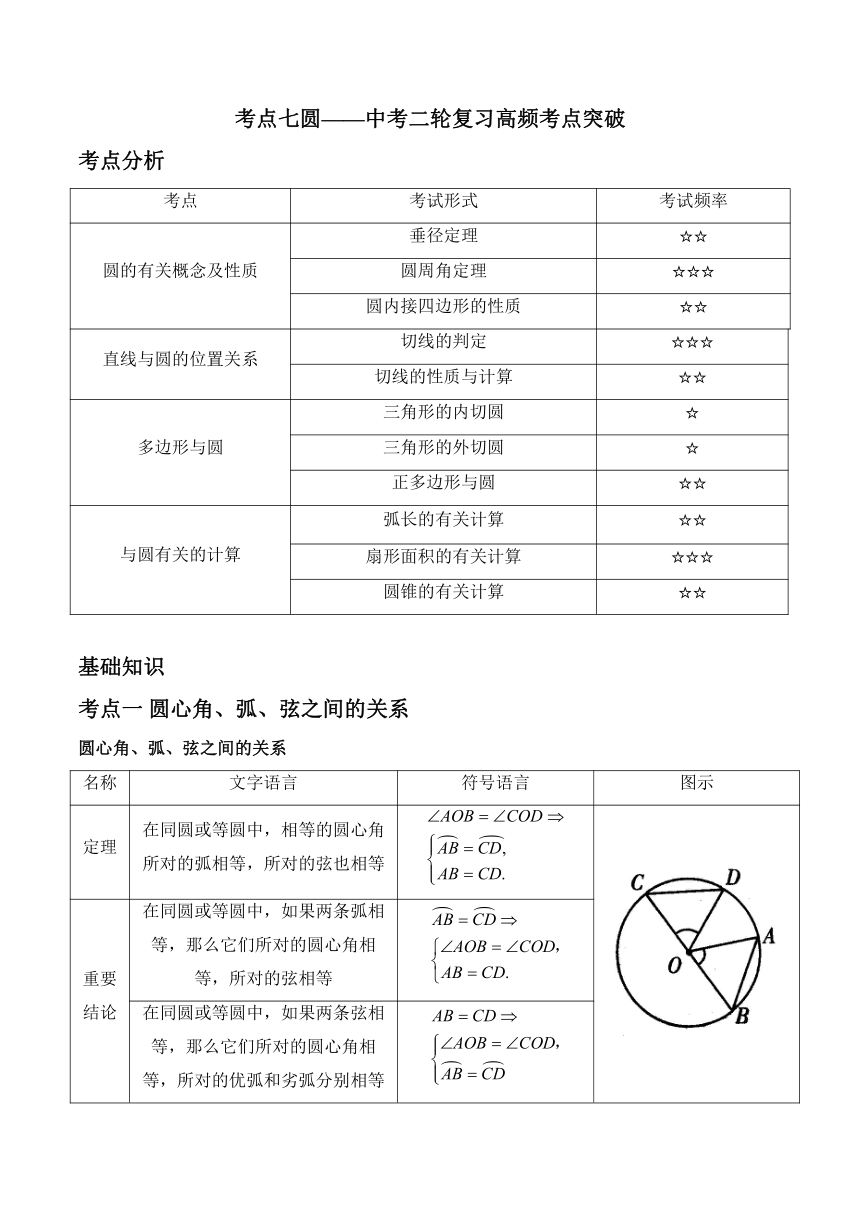
考点七圆———中考二轮复习高频考点突破 考点分析 考点 考试形式 考试频率 圆的有关概念及性质 垂径定理 圆周角定理 圆内接四边形的性质 直线与圆的位置关系 切线的判定 切线的性质与计算 多边形与圆 三角形的内切圆 三角形的外切圆 正多边形与圆 与圆有关的计算 弧长的有关计算 扇形面积的有关计算 圆锥的有关计算 基础知识 考点一 圆心角、弧、弦之间的关系 圆心角、弧、弦之间的关系 名称 文字语言 符号语言 图示 定理 在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等 重要结论 在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等 在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优弧和劣弧分别相等 考点二 圆周角定理及其推论 名称 文字语言 符号语言 图示 定理 一条弧所对的圆周角等于它所对的圆心角的一半. 是所对的一个圆周角,是所对的圆心角,那么 推论 同弧或等弧所对的圆周角相等. 都是所对的圆周角,那么 半圆(或直径)所对的圆周角是直角,的圆周角所对的弦是直径. 若为直径,则;若或..,则为直径. 考点三 垂径定理及其推论 1.垂径定理及其推论 名称 文字语言 符号语言 图示 垂径定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧. 垂径定理的推论 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 考点四 点、直线与圆的位置关系 1.点和圆的位置关系 点和圆的位置关系分三种(设的半径为,点到圆心的距离): 点和圆的位置关系 特点 性质及判定 图示 点在圆外 点到圆心的距离大于半径 点在圆外. 点在圆上 点到圆心的距离等于半径 点在圆上. 点在圆内 点到圆心的距离小于半径 点在圆内. 2.直线和圆的位置关系 直线和圆的位置关系 相交 相切 相离 定义 直线和圆有两个公共点,这时我们说这条直线和圆相交. 直线和圆只有一个公共点,这时我们说这条直线和圆相切. 直线和圆没有公共点,这时我们说这条直线和圆相离. 图示 公共点个数 2 1 0 圆心到直线的距离与半径的关系 公共点名称 交点 切点 直线名称 割线 切线 考点五 切线的性质与判定 1.切线的判定定理和性质定理 切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.如图所示,是的半径,若于点,则是的切线. 切线的性质定理:圆的切线垂直于过切点的半径.如图,若切于点,则. 2.切线长及切线长定理 切线长:经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长. 切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 【注意】经过圆上一点作圆的切线,有且只有一条;经过圆外一点作圆的切线,有两条. 考点六 三角形的外接圆与内切圆 1.三角形的外接圆 三角形的外接圆:经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,这个三角形叫做这个圆的内接三角形. 三角形的外心:三角形的外接圆的圆心是三角形三条边的垂直平分线的交点,叫做这个三角形的外心. 三角形外心的性质:三角形的外心到三角形三个顶点的距离相等,等于其外接圆的半径. 2.三角形的内切圆 三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆,这个三角形叫做这个圆的外切三角形. 三角形的内心:三角形的内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心. 三角形内心的性质:三角形的内心到三角形三条边的距离相等,且等于其内切圆的半径. 考点七 与圆有关的计算 1.弧长公式 在半径为的圆中,因为的圆心角所对的弧长就是圆周长,所以的圆心角所对的弧长是,即.于是的圆心角所对的弧长为. 2.扇形面积公式 (1)在半径为的圆中,因为的圆心角所对的扇形的面积就是圆面积,所以圆心角是的 ... ...
~~ 您好,已阅读到文档的结尾了 ~~