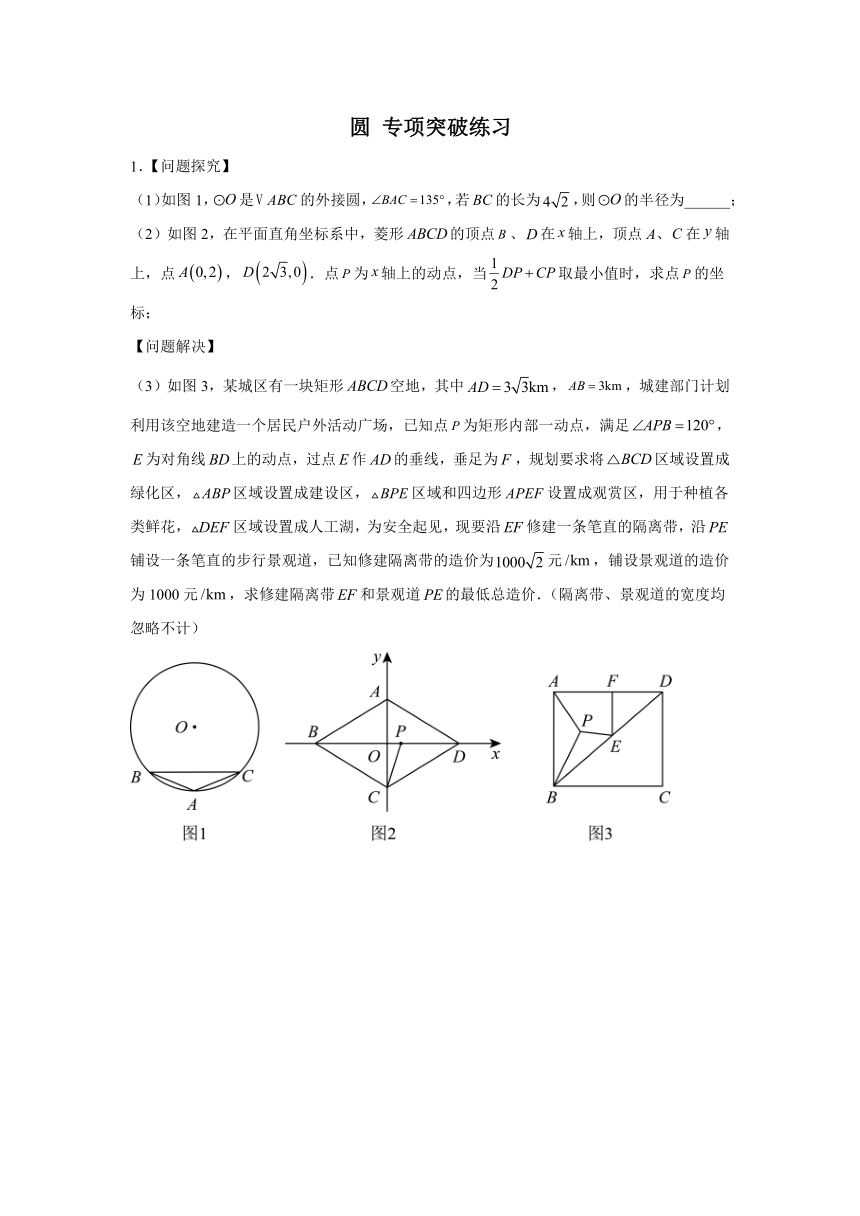
圆 专项突破练习 1.【问题探究】 (1)如图1,是的外接圆,,若的长为,则的半径为_____; (2)如图2,在平面直角坐标系中,菱形的顶点、在轴上,顶点A、在轴上,点,.点为轴上的动点,当取最小值时,求点的坐标; 【问题解决】 (3)如图3,某城区有一块矩形空地,其中,,城建部门计划利用该空地建造一个居民户外活动广场,已知点为矩形内部一动点,满足,为对角线上的动点,过点作的垂线,垂足为,规划要求将区域设置成绿化区,区域设置成建设区,区域和四边形设置成观赏区,用于种植各类鲜花,区域设置成人工湖,为安全起见,现要沿修建一条笔直的隔离带,沿铺设一条笔直的步行景观道,已知修建隔离带的造价为元,铺设景观道的造价为1000元,求修建隔离带和景观道的最低总造价.(隔离带、景观道的宽度均忽略不计) 2.如图,是正方形的外接圆. (1)如图1,若是上的一点,Q是上的一点,且. ①求证:. ②若,求的直径. (2)如图2,若点P在上,过点作,求证:. 3.如图1,在锐角内找一点,过点作于点,以为直径作,过点作于点,延长交于点,连接. (1)若,则_____; (2)如图2,若,点在的延长线上,求证:是的切线; (3)如图3,连接,若于点,且,求的值. 4.【新知引入】定义:如图(1),点M,N把线段分割成和,若以为边的三角形是一个直角三角形,则称点M,N是线段的勾股分割点. (1)已知点M,N是线段的勾股分割点,若,则_____. 【探究证明】 (2)如图(2),在中,,M,N在线段上,且.求证:点M,N是线段的勾股分割点. 【拓展应用】 (3)如图(3),在中,圆心角,P是上一动点,连接,分别作的垂直平分线,分别交直线于点C,D,已知,当是以为底边的等腰三角形时,请直接写出线段的长. 5.在中,,,点D为的中点.将绕点D逆时针旋转得到,旋转角为,过点作(以为直径)的切线,切点为F. 【知识技能】 (1)如图1,若旋转角,求证:; 【数学理解】 (2)如图2,若旋转角,求点到的距离; 【拓展探索】 (3)在旋转过程中,当直线时,求旋转角的度数. 6.如图1,以的直角边为直径作,交斜边于点D,E是的中点,连接,. (1)求证:是的切线. (2)如图2,点F在的延长线上,点M在线段上,于点N,交于点G.求证:. (3)在(2)的条件下,若,求的面积. 7.定义:中,是它的中线,点在上,若,则称是的“陪位中线”. (1)如图,在中,,是的中点,,垂足为,求证:是的“陪位中线”; (2)内接于,是的中点,连接. 如图,点在上,连接交于点,连接,,若是的“陪位中线”,请从以下的结论中,选择一个正确的结论并给予证明; ⅰ); ⅱ)是的“陪位中线”; ⅲ); 如图,过点作的切线交延长线于点,连接交于点,请判断是否为的“陪位中线”,并说明理由. 8.如图1,是的外接圆,是的直径,点是上一点,连接交于点,过点作,交于点,交的延长线于点. (1)求证:; (2)如图2,连接, ①若,,求的长度; ②如图3,若点是的中点,过点作交的延长线于点, 求证:. 9.已知,四边形内接于,对角线交于H,. (1)如图1,求证:; (2)如图2,作直径交于点F,连接,,求证:; (3)如图3,在(2)的条件下,在上截取,于点Q,交于L,若,,求的长. 10.综合与实践 【课本再现】 (1)如图1,的和的平分线相交于点G. ①若,则_____; ②求证:. 【数学思考】 (2)如图2,中的平分线与其外角的平分线交于点O,猜想与之间的数量关系,并给予证明. 【问题解决】 (3)如图3,菱形的顶点在上,与相交于点为的中点,若,求的值. 《圆压轴题专项突破练习-2025年中考数学二轮专题》参考答案 1.(1)4;(2)点的坐标为;(3)元 【分析】(1)如图:在上取一点D,连接,根据圆的内接四边形的性质可得,再根据圆周角 ... ...
~~ 您好,已阅读到文档的结尾了 ~~