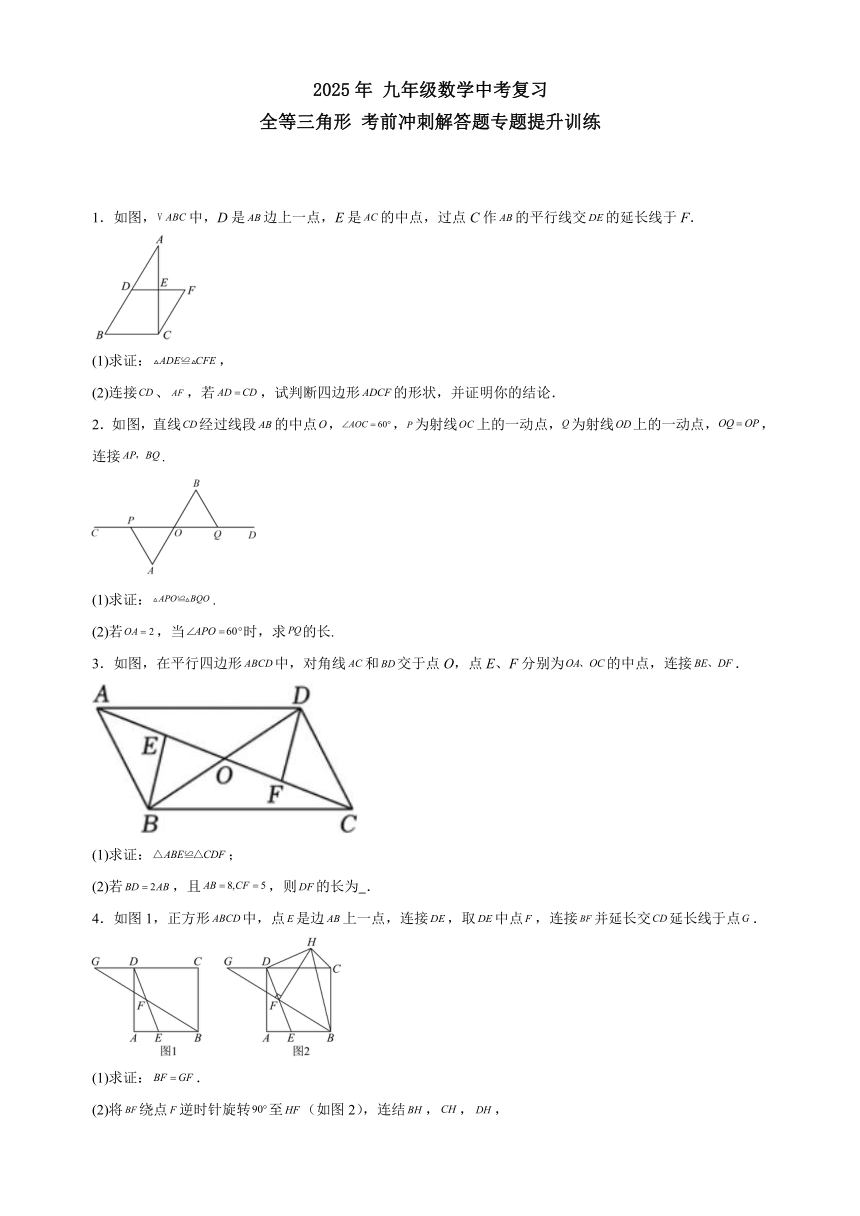
2025年九年级数学中考复习全等三角形考前冲刺解答题专题提升训练（含解析）

2025年 九年级数学中考复习 全等三角形 考前冲刺解答题专题提升训练 1．如图，中，D是边上一点，E是的中点，过点C作的平行线交的延长线于F． (1)求证：， (2)连接、，若，试判断四边形的形状，并证明你的结论． 2．如图，直线经过线段的中点，，为射线上的一动点，为射线上的一动点，，连接. (1)求证：. (2)若，当时，求的长. 3．如图，在平行四边形中，对角线和交于点O，点E、F分别为的中点，连接． (1)求证：； (2)若，且，则的长为 ． 4．如图1，正方形中，点是边上一点，连接，取中点，连接并延长交延长线于点． (1)求证：． (2)将绕点逆时针旋转至（如图2），连结，，， ①求的度数； ②求证：． 5．如图，点E、C、D、A在同一条直线上，，，，线段与线段交于点G． (1)求证：； (2)若，，求的度数． 6．如图1，在中，，平分，点E在斜边边上，以为直径的经过点D． (1)求证：直线为的切线． (2)如图2，连结，若，，求的长． 7．如图，在中，，，，P为边上的动点，过点P在上方作，使，以，为邻边作． (1)当点F落在上时，如图（2），求的长． (2)当的中点M落在上时，如图（3），设交于点N，求证：． (3)连接，在点P从点A向点B运动的过程中，沿直线将剪开，当剪开的两部分可以拼成一个不重叠无缝隙的三角形时，直接写出的长（写出两个即可）． 8．古希腊数学家帕波斯在《数学汇编》中探讨了旋转构造下的几何关系．已知，在中，，，，点P为直线上一动点（不与点A，B重合），连接，将线段绕点P顺时针旋转得到线段，旋转角为，连接． (1)当点P在延长线上如图①，探究线段与的数量关系； (2)当点P在直线上，且，，时，请求出线段的长． 9．已知两个完全重叠放置的三角形纸片和，，， ．现将绕点逆时针旋转，旋转角为． (1)如图1，当的直角顶点恰好落在边上时，延长交于点，求证：点在的平分线上． (2)当将绕点逆时针旋转到任意位置（如图2）时，延长交于点，请判断点是否为的中点，并说明理由． (3)如图3，当的直角顶点恰好落在的中线的延长线上时，延长交于点，请直接写出此时的长． 10．如图1，和，点在同一条直线上，已知． (1)求证：； (2)如图2，连接，请判断四边形的形状，并说明理由． 11．已知点是矩形的边上一点，连接，将矩形沿翻折，使点，分别落在，处． (1)如图1，连接，为的中点，，求证：； (2)如图2，点，，共线，，的延长线相交于点，连接， ①若，求的值； ②点，分别是，延长线上的点，，连接，，若，求证：平分． 12．在矩形中，点是边的中点，点是边上的点，的延长线与的延长线交于点，以为斜边向下作等腰直角． (1)如图1，求证：； (2)若点为的中点， 如图，当在上时，求； 如图，连接，当，时，求的长． 13．如图①，在中，，，，，分别是，的中点，连接．将绕点逆时针旋转得到，点，的对应点分别是，，直线与边交于点（不与点、重合）． (1)观察发现 线段的长为_____；在绕点旋转的过程中，与的数量关系为_____； (2)探究迁移 当点、、三点共线时，如图②，求的长； (3)拓展应用 在绕点旋转的过程中，与交于点，当与的一边平行时，请直接写出的长． 14．在中，，，点D为平面内一点（A，B，D三点不共线），为的中线． 【问题初探】 （1）如图1，延长至点M，使得，连接，则与的数量关系为 ； 【类比探究】 （2）如图2，将绕点A顺时针旋转得到，连接．请你猜想与的数量关系，并证明你的结论； 【拓展延伸】 （3）如图3，在（2）的条件下，点D在以点A为圆心，长为半径的圆上运动，直线与直线交于点G，连接，在点G的运动过程中存在最大值．若请直接写出的最大值． 15．在和中，，，，． (1)如图，求证：； (2)当点落在线段上时． 如图，若平分时，，求线段的长； 如图，是的中点，过点作交于点，当时，判断线段 ... ...