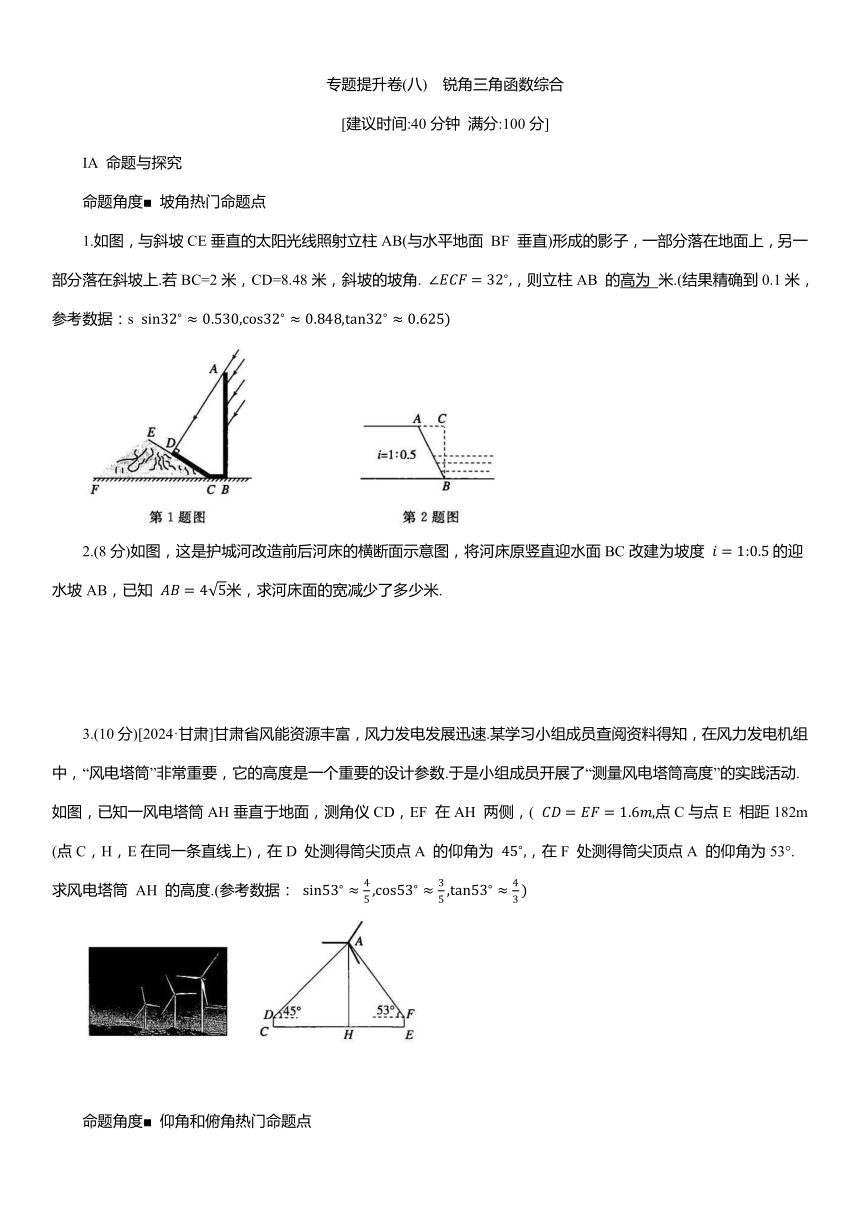
专题提升卷(八) 锐角三角函数综合 [建议时间:40分钟 满分:100分] IA 命题与探究 命题角度■ 坡角热门命题点 1.如图,与斜坡CE垂直的太阳光线照射立柱AB(与水平地面 BF 垂直)形成的影子,一部分落在地面上,另一部分落在斜坡上.若BC=2米,CD=8.48米,斜坡的坡角. ,则立柱AB 的高为 米.(结果精确到0.1米,参考数据:s 2.(8分)如图,这是护城河改造前后河床的横断面示意图,将河床原竖直迎水面BC改建为坡度 的迎水坡AB,已知 米,求河床面的宽减少了多少米. 3.(10分)[2024·甘肃]甘肃省风能资源丰富,风力发电发展迅速.某学习小组成员查阅资料得知,在风力发电机组中,“风电塔筒”非常重要,它的高度是一个重要的设计参数.于是小组成员开展了“测量风电塔筒高度”的实践活动.如图,已知一风电塔筒AH垂直于地面,测角仪CD,EF 在AH 两侧,( 点C与点E 相距182m(点C,H,E在同一条直线上),在D 处测得筒尖顶点A 的仰角为 ,在F 处测得筒尖顶点A 的仰角为53°.求风电塔筒 AH 的高度.(参考数据: 命题角度■ 仰角和俯角热门命题点 4.如图,某数学实践小组测量操场的旗杆AB的高度,操作如下: (1)在点 D 处放置测角仪,量得测角仪的高度CD为a; (2)测得仰角 (3)量得测角仪到旗杆的水平距离 BD 为b. 则旗杆的高度可表示为 ( ) A. a+btanα 5.(10分)如图,某数学活动小组用高度为1.5米的测角仪 BC,对垂直于地面CD的建筑物AD的高度进行测量,BC⊥CD 于点C.在 B 处测得A 的仰角. 然后将测角仪向建筑物方向水平移动6米至 FG处,FG⊥CD 于点G,测得A 的仰角∠AFE=58°,BF的延长线交AD 于点E,求建筑物 AD的高度.(结果保留小数点后一位,参考数据: 命题角度目 方向角热门命题点 6.如图,一艘轮船航行至O点时,测得某灯塔A 位于它的北偏东40°方向,且它与灯塔A 相距13 海里,继续沿正东方向航行,航行至点B 处时,测得灯塔A恰好在它的正北方向,则AB的距离可表示为 ( ) A.13cos40°海里 B.13sin40°海里 海里 海里 7.(10分)[2024·北京]如图,海中有一个小岛C,某渔船在海中的A 点测得小岛C位于东北方向上,该渔船由西向东航行一段时间后到达 B点,此时测得小岛 C位于北偏西30°方向上,再沿北偏东60°方向继续航行一段时间后到达 D点,这时测得小岛 C位于北偏西 60°方向上.已知 A,C相距30 n mile.求C,D间的距离.(计算过程中的数据不取近似值) 命题角度四 锐角三角函数综合热门命题点 8.如图,在铁路建设中,需要确定隧道两洞口 A 和B 之间的距离.点D,点E分别位于测绘点C的正北和正西方向.已知测得两定位点 E 和D 与隧道口A 和B 的距离分别为150m和100m,测绘点 H,G分别为CD,CE的中点,测绘方在测绘点 H测得点G 在点H 的南偏西53°的方向上,且 HC=480m,则隧道AB 的长约为 米.(参考数据: 9.[2024·湖南] 如图,图1 为《天工开物》记载的用于舂(chōng)捣谷物的工具———�碓(duì)”的结构简图,图 2 为其平面示意图.已知AB⊥CD 于点 B,AB 与水平线l 相交于点O,OE⊥l.若 BC=4分米,OB=12分米,∠BOE=60°,则点 C到水平线l的距离CF 为 分米.(结果用含根号的式子表示) 10.(10分)[2024·广东]中国新能源汽车为全球应对气候变化和绿色低碳转型作出了巨大贡献.为满足新能源汽车的充电需求,某小区增设了充电站,如图,这是矩形 PQMN 充电站的平面示意图,矩形 ABCD 是其中一个停车位.经测量,∠ABQ=60°,AB=5.4m,CE=1.6m,GH⊥CD,GH是另一个车位的宽,所有车位的长宽相同,按图示并列划定.根据以上信息回答下列问题.(结果精确到0.1m,参考数据: (1)求 PQ的长. (2)若该充电站有20个停车位,求PN 的长. B仿 真 与 预 测 11.如图,飞机在空中A处探测到它的正下方地面上目标C,此时飞行高度AC=1200米,从飞机上看地面指挥台B的俯角α的正切值为 ,则飞 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

