浙教版2024-2025学年数学七年级下册 第1章 相交线与平行线 单元练习（无答案）

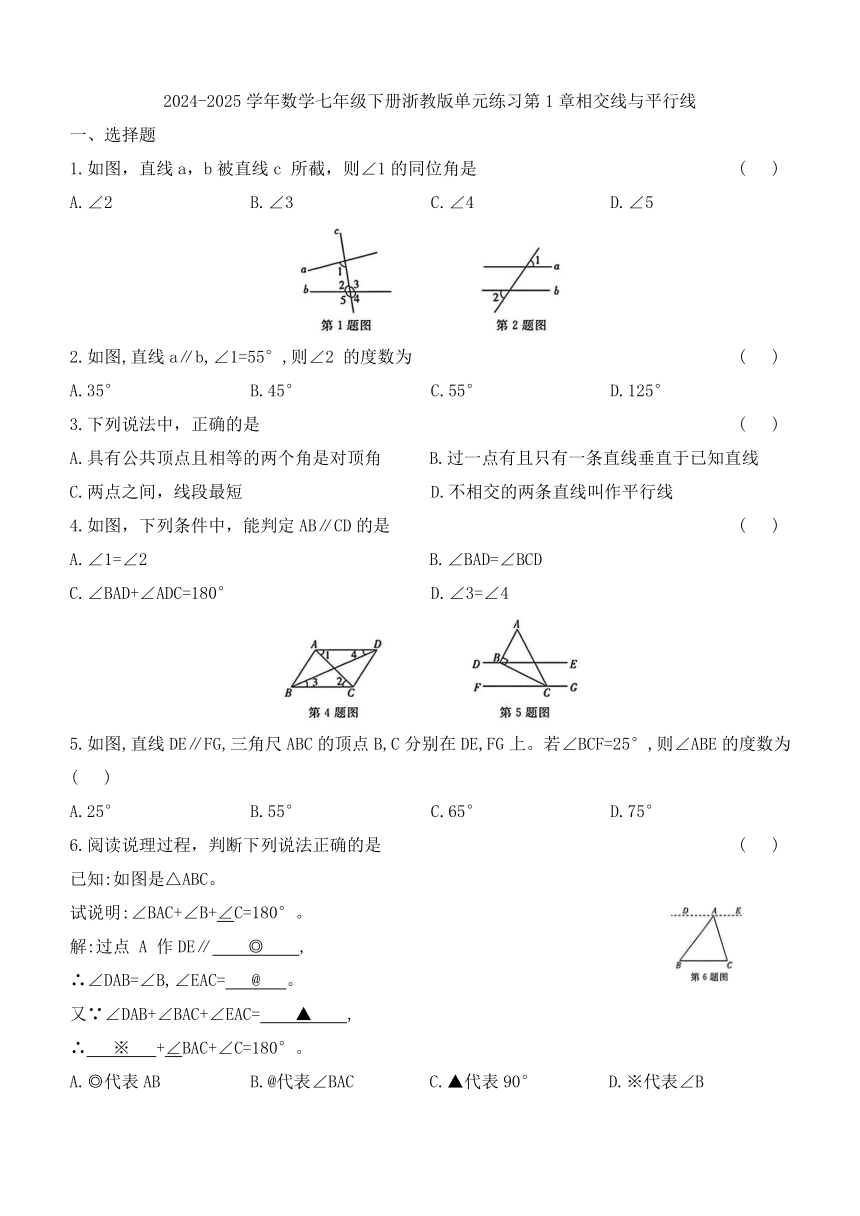
2024-2025学年数学七年级下册浙教版单元练习第1章相交线与平行线 一、选择题 1.如图，直线a，b被直线c 所截，则∠1的同位角是 ( ) A.∠2 B.∠3 C.∠4 D.∠5 2.如图,直线a∥b,∠1=55°,则∠2 的度数为 ( ) A.35° B.45° C.55° D.125° 3.下列说法中，正确的是 ( ) A.具有公共顶点且相等的两个角是对顶角 B.过一点有且只有一条直线垂直于已知直线 C.两点之间，线段最短 D.不相交的两条直线叫作平行线 4.如图，下列条件中，能判定AB∥CD的是 ( ) A.∠1=∠2 B.∠BAD=∠BCD C.∠BAD+∠ADC=180° D.∠3=∠4 5.如图,直线DE∥FG,三角尺ABC的顶点B,C分别在DE,FG上。若∠BCF=25°,则∠ABE的度数为( ) A.25° B.55° C.65° D.75° 6.阅读说理过程，判断下列说法正确的是 ( ) 已知:如图是△ABC。 试说明:∠BAC+∠B+∠C=180°。 解:过点 A 作DE∥ ◎ , ∴∠DAB=∠B,∠EAC= @ 。 又∵∠DAB+∠BAC+∠EAC= ▲ , ∴ ※ +∠BAC+∠C=180°。 A.◎代表AB B.@代表∠BAC C.▲代表90° D.※代表∠B 7.若要求作业纸上两条相交直线AB，CD所夹锐角的度数，但其交点不在作业纸内，无法直接测量，两同学提供了如下间接测量的方案： 方案Ⅰ 方案Ⅱ ①作一直线GH,分别交 AB,CD于点E,F。 ①作一直线GH,分别交AB,CD于点E,F。 ②作∠HEN=∠CFG。 ②测量∠AEH,∠CFG的度数。 ③测量∠AEM的度数即可。 ③计算|180°-∠AEH-∠CFG|即可。 对于方案Ⅰ，Ⅱ，下列说法正确的是 ( ) A.Ⅰ可行，Ⅱ不可行 B.Ⅰ不可行，Ⅱ可行 C.Ⅰ,Ⅱ都可行 D.Ⅰ,Ⅱ都不可行 8.小明观察“抖空竹”时发现，可以将某一时刻的情形抽象成几何图形：如图，已知AB∥CD，∠BAE=91°，∠DCE=124°,则∠AEC的度数为 ( ) A.29° B.30° C.31° D.33° 9.如图，将网格中的三条线段沿网格线的方向(水平或竖直)平移后组成一个首尾依次相接的三角形，至少需要移动 ( ) A.12格 B.11格 C.9格 D.8格 10.如图,已知AB∥EG,BC∥DE,CD∥EF,则∠x,∠y,∠z三者之间的关系是 ( ) A.∠x+∠y+∠z=180° B.∠x-∠z=∠y C.∠y-∠x=∠z D.∠y-∠x=∠x-∠z 二、填空题 11.如图，与∠1是同旁内角的是 ，与∠2是内错角的是 。 12.如图，下列条件中，能判定AB∥CD的是 (填序号)。 ①∠B+∠BAD=180°;②∠1=∠2;③∠3=∠4;④∠5+∠1+∠3=180°。 13.如图,已知AB∥CE,∠B=50°,CE平分∠ACD,则∠ACD的度数为 °。 14.如图,已知直线a⊥c,b⊥c。若∠1=110°,则∠2的度数为 °。 15.如图，将一张长方形纸片沿 EF折叠后，点 A，B 分别落在点A'，B'的位置。若∠2=70°，则∠1的度数为 °。 16.如图1，一块长为a(cm)，宽为b(cm)的长方形地板中间有一条裂缝。如图2，若把裂缝右边的一块向右平移x(cm),则产生的裂缝的面积为 cm 。 三、解答题 17.如图，在方格纸中，有两条线段AB，BC。利用方格纸完成以下操作： (1)过点 A 作BC 的平行线。 (2)过点 C作AB 的平行线，与(1)中的平行线相交于点 D。 (3)过点 B 作BC 的垂线l。 18.如图，潜望镜中的两面镜子AB，CD是互相平行放置的，光线经过镜子反射时，请说明进入潜望镜的光线l 和离开潜望镜的光线l 平行。 解:∵AB∥CD(已知), ∴∠2= ( )。 ∵∠1=∠2,∠3=∠4(已知), ∴∠1=∠2=∠3=∠4(等量代换), ∴∠1+∠2=∠3+∠4。 ∵∠1+∠2+∠5=180°(平角的定义), 。 同理 ∴ = (等量代换), 19.如图,直线AB,CD相交于点 O, ，且 求 的度数。 20.如图,在三角形ABC中,AC=4 cm,BC=3cm,将三角形ABC沿AB 方向平移得到三角形DEF,连结CF。 若AE=8cm,DB=2cm,求: (1)三角形ABC沿AB 方向平移的距离。 (2)四边形AEFC的周长。 21.如图,AD∥BC,∠DAC=127°,∠ACF=15°,∠EFC=142°。 (1)试说明:EF∥AD。 (2)连结CE,若CE平分∠BCF,求∠FEC的度数。 22.如图,已知点A在EF 上,点 P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ。 ... ...