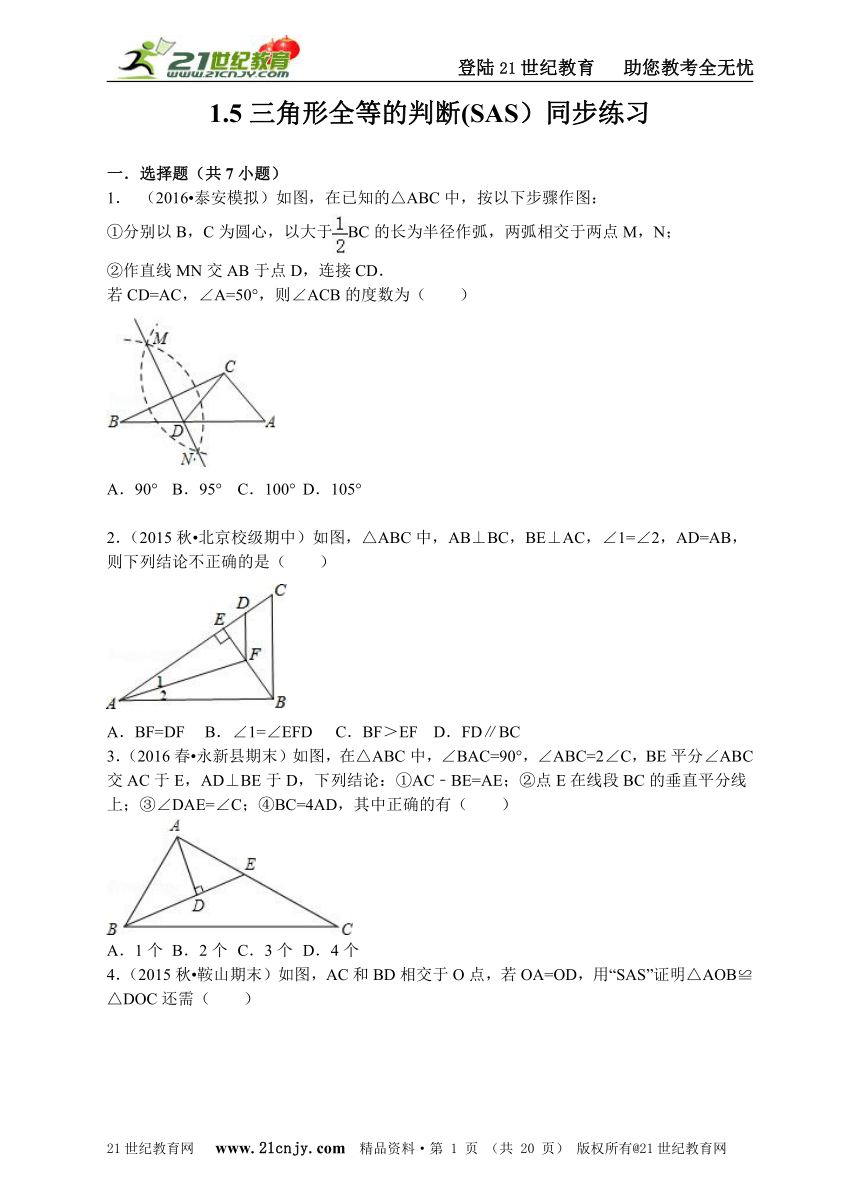
1.5三角形全等的判断(SAS）同步练习

1.5三角形全等的判断(SAS）同步练习 　 一．选择题（共7小题） 1． （2016?泰安模拟）如图，在已知的△ABC中，按以下步骤作图： ①分别以B，C为圆心，以大于BC的长为半径作弧，两弧相交于两点M，N； ②作直线MN交AB于点D，连接CD． 若CD=AC，∠A=50°，则∠ACB的度数为（　　） A．90° B．95° C．100° D．105° 2．（2015秋?北京校级期中）如图，△ABC中，AB⊥BC，BE⊥AC，∠1=∠2，AD=AB，则下列结论不正确的是（　　）21·cn·jy·com A．BF=DF B．∠1=∠EFD C．BF＞EF D．FD∥BC 3．（2016春?永新县期末）如图，在△ABC中，∠BAC=90°，∠ABC=2∠C，BE平分∠ABC交AC于E，AD⊥BE于D，下列结论：①AC﹣BE=AE；②点E在线段BC的垂直平分线上；③∠DAE=∠C；④BC=4AD，其中正确的有（　　） A．1个 B．2个 C．3个 D．4个 4．（2015秋?鞍山期末）如图，AC和BD相交于O点，若OA=OD，用“SAS”证明△AOB≌△DOC还需（　　）2·1·c·n·j·y A．AB=DC B．OB=OC C．∠C=∠D D．∠AOB=∠DOC 5．（2015秋?绵竹市期末）如图，∠BAC=110°，若MP和NQ分别垂直平分AB和AC，则∠PAQ的度数是（　　） A．20° B．40° C．50° D．60° 6．（2016?天门）如图，在△ABC中，AC的垂直平分线分别交AC、BC于E，D两点，EC=4，△ABC的周长为23，则△ABD的周长为（　　） A．13 B．15 C．17 D．19 7．（2015?邗江区二模）如图，△ABC中，AB=AC，BD=CE，BE=CF，若∠A=40°，则∠DEF的度数是（　　）【出处：21教育名师】 A．75° B．70° C．65° D．60° 二．填空题（共2小题）　 8．（2015?娄底）如图，已知AB=BC，要使△ABD≌△CBD，还需添加一个条件，你添加的条件是　　　　．（只需写一个，不添加辅助线） 　 9．（2015秋?上城区期中）已知：如图，点B、F、E、C在同一条直线上，AB∥CD，且AB=CD，BF=CE． 求证：∠AEB=∠DFC． 证明：∵AB∥CD（已知）， ∴∠B=∠C（　　　　） ∵BF=CE（已知）， ∴BF+　　　　=CE+　　　　，即BE=CF． 在△ABE和△DCF中， ∴△ABE≌△DCF（ ）． ∴∠AEB=∠DFC． 三．解答题（共13小题） 10.（2015秋?东西湖区期中）如图，点D在BC上，∠1=∠2，AE=AC，下面三个条件：①AB=AD；②BC=DE；③∠E=∠C，请你从所给条件①②③中选一个条件，使△ABC≌△ADE，并证明两三角形全等． 11．（2015秋?简阳市期末）如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．如果点P在线段BC上以3cm/s的速度由B点向C点运动，同时，点Q在线段CA上由C点向A点运动． （1）若点Q的运动速度与点P的运动速度相等，经过1s后，△BPD与△CQP是否全等，请说明理由； （2）若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPD与△CQP全等？ 12．（2016?云南模拟）在△ABC中，AB=AC，点E，F分别在AB，AC上，AE=AF，BF与CE相交于点P．求证：△EBC≌△FCB． 13．（2016?历城区二模）如图，AB=CB，BE=BF，∠1=∠2，证明：△ABE≌△CBF． 14．（2014?惠安县一模）已知：如图，点E，C在线段BF上，AB=DE，AB∥DE，BE=CF．求证：AC=DF． 15．（2016?曲靖）如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D． （1）求证：AC∥DE； （2）若BF=13，EC=5，求BC的长． 16．（2014秋?仙游县校级月考）已知，如图，AC=AD，BC=BD，O为AB上一点， 求证：OC=OD． 17．如图在△ABC中，AB=AC，∠BAC=90°，D是BC上的一点，EC⊥BC，EC=BD （1）证明：△ABD≌△ACE； （2）证明：AD⊥AE； （3）若AF⊥DE，F为垂足，AG=GC，则FG与AC有怎样的位置关系，请说明理由． 18．如图，△ABC中，∠BAD=90°，AB=AD，△ACE中，∠CAE=90°，AC=AE． （1）求证：△ACD≌AEB； （2）试判断∠AFD和∠AFE的大小关系，并说明理由． 19．（20 ... ...