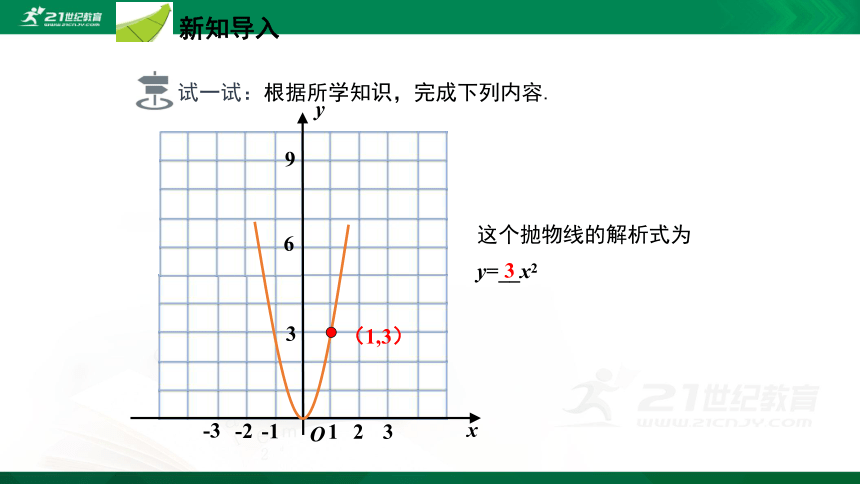
新知导入 试一试:根据所学知识,完成下列内容. -1 -2 -3 9 3 6 1 2 3 y O x (1,3) 这个抛物线的解析式为 y=__x2 3 新知导入 试一试:根据所学知识,完成下列内容. -1 -2 -3 9 3 6 1 2 3 y O x (2,3) 这个抛物线的解析式为 y=__(x-__)2 3 1 新知导入 试一试:根据所学知识,完成下列内容. -1 -2 -3 9 3 6 1 2 3 y O x (1,2) 这个抛物线的解析式为 y=__(x-__)2+___ 3 1 2 确定二次函数的表达式 1.体会确定二次函数表达式所需要的条件. 2.体会用待定系数法确定二次函数表达式. 学习目标 初步探究确定二次函数表达式所需要的条件 如图所示,这是一名学生推铅球时,铅球行进高度y(m)与水平距离x(m)之间的图象,你能求出其表达式吗? 解: 如图所示,(4,3)是抛物线的顶点坐标, ∴设二次函数表达式为y=a(x-4)2+3, 把点(10,0)代入y=a(x-4)2+3,解得a= , 因此铅球行进高度y(m)与水平距离x(m)之间的函数表达式为y= . 总结: (1)形如y=ax2的二次函数,因为只有一个系数a是未知的,所以只需要知道图象上一个点的坐标即可. (2)形如y=a(x-h)2和y=ax2+k的二次函数,有两个系数是未知的,所以需要知道图象上两个点的坐标即可. (3)形如y=a(x-h)2+k的二次函数,如果已知二次函数的顶点坐标,那么再知道图象上的一个点的坐标就可以确定二次函数的表达式. 二次函数表达式的确定方法 例1 已知二次函数y=ax2+c的图象经过点(2,3)和(-1,-3),求这个二次函数的表达式. 〔解析〕由于函数图象经过点(2,3)和(-1,-3),所以直接把两个点的坐标代入y=ax2+c,得到关于a和c的二元一次方程组,解方程组得出a,c的值即可. 解:将点(2,3)和(-1,-3)的坐标分别代入表达式y=ax2+c,得 解这个方程组,得 所以,所求二次函数表达式为y=2x2-5. 【做一做】 已知二次函数的图象与y轴交点的纵坐标为1,且经过点(2,5)和(-2,13),求这个二次函数的表达式. 思考下面的问题: 1.二次函数y=ax2+bx+c的图象与y轴的交点坐标是什么? 2. 二次函数y=ax2+bx+c的图象与y轴交点的纵坐标与系数c有什么关系? 3.二次函数表达式y=ax2+bx+c中除了系数c之外,还有几个未知系数? 解:因为二次函数图象与y轴交点的纵坐标为1,所以c=1. 设二次函数的表达式为y=ax2+bx+1,将点(2,5)和(-2,13)代入y=ax2+bx+1,得 解得 所以所求二次函数的表达式为y=2x2-2x+1. 【做一做】 已知二次函数的图象与y轴交点的纵坐标为1,且经过点(2,5)和(-2,13),求这个二次函数的表达式. 归纳确定二次函数表达式所需要的条件 【想一想】 在什么情况下,已知二次函数图象上两点的坐标就可以确定它的表达式? 总结: 1.二次函数y=ax2+bx+c可化成:y=a(x-h)2+k,顶点坐标是(h,k),如果已知顶点坐标,那么再知道图象上的一个点的坐标就可以确定二次函数的表达式. 确定表达式的步骤和方法: 设表达式为顶点式:y=a(x-h)2+k,再把另一个点的坐标代入,求出a的值,就可以确定所求二次函数的表达式. 2.已知二次函数y=ax2+bx+c中一项系数,再知道图象上的任意两个点的坐标,也可以确定二次函数的表达式. 确定表达式的步骤和方法: 把两个点的坐标代入表达式,得到二元一次方程组,解这个方程组,得到两个未知系数的值,就可以确定所求二次函数的表达式 课程讲授 1 利用“一般式”求二次函数的解析式 问题1:我们已经知道由两点就可以确定一条直线,那么由几个点的坐标就可以确定二次函数呢? y = a x2 + b x + c 含有____个待定系数,需要____个抛物线上的点的坐标就能求出来其解析式. 3 3 课程讲授 1 利用“一般式”求二次函数的解析式 问题1:已经知道一条抛物线的图象经过(-1,10),(1,4),(2,7)三点,请你根据所学知识求出这条抛物线的解析式. 解 过设所求二次函数为y=ax2+bx+c 由已知,函数图图象经经过(-1,10),(1,4),(2,7)三点, 得到关于a,b,c的三元一次方程 ... ...
~~ 您好,已阅读到文档的结尾了 ~~