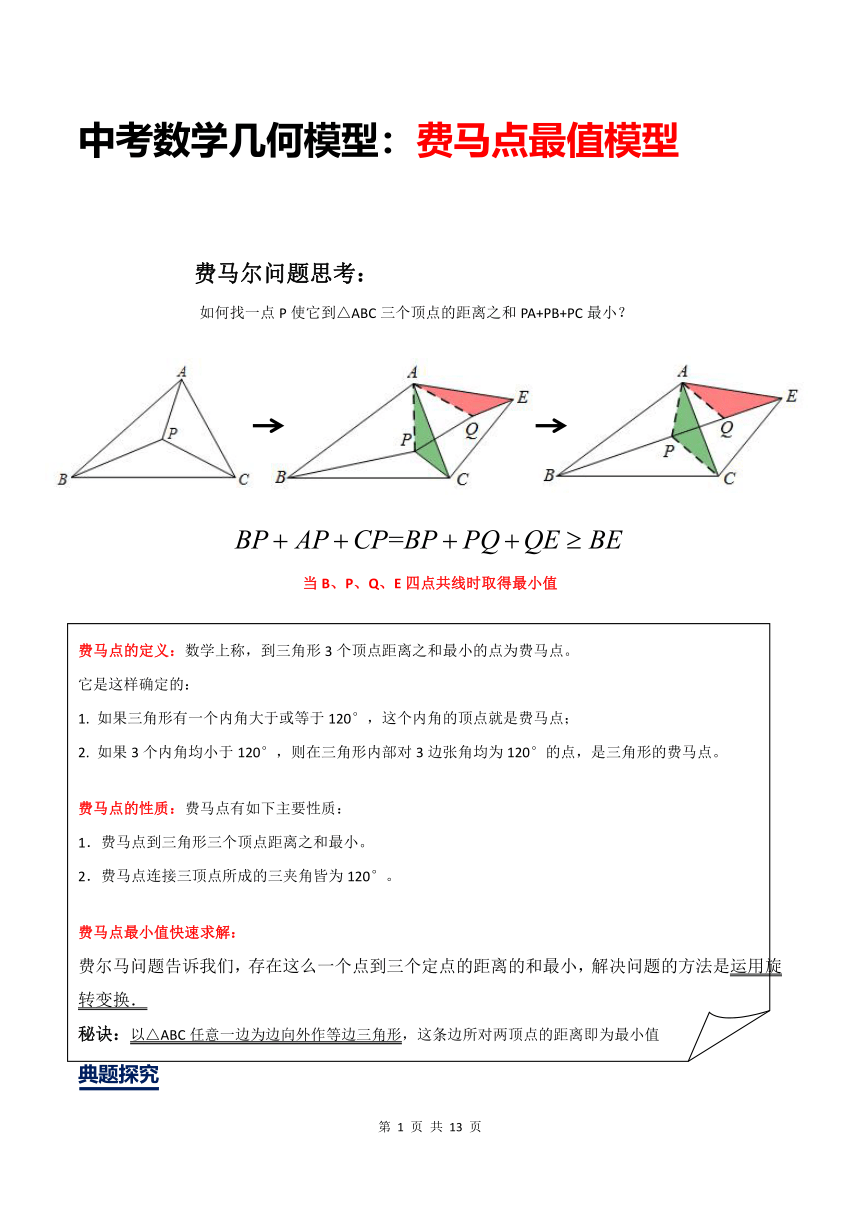
中考数学几何模型：费马点最值模型（Word版，附答案）

中考数学几何模型：费马点最值模型 费马尔问题思考： 如何找一点P使它到△ABC三个顶点的距离之和PA+PB+PC最小？ 当B、P、Q、E四点共线时取得最小值 费马点的定义：数学上称，到三角形3个顶点距离之和最小的点为费马点。 它是这样确定的： 1. 如果三角形有一个内角大于或等于120°，这个内角的顶点就是费马点； 2. 如果3个内角均小于120°，则在三角形内部对3边张角均为120°的点，是三角形的费马点。 费马点的性质：费马点有如下主要性质： 1．费马点到三角形三个顶点距离之和最小。 2．费马点连接三顶点所成的三夹角皆为120°。 费马点最小值快速求解： 费尔马问题告诉我们，存在这么一个点到三个定点的距离的和最小，解决问题的方法是运用旋转变换． 秘诀：以△ABC任意一边为边向外作等边三角形，这条边所对两顶点的距离即为最小值 典题探究 例题1. 已知：△ABC是锐角三角形，G是三角形内一点。∠AGC=∠AGB=∠BGC=120°. 求证：GA+GB+GC的值最小. 证明：将△BGC逆时针旋转60°，连GP,DB.则 △CGB≌△CPD； ∴ ∠CPD=∠CGB=120°,CG=CP,GB=PD, BC=DC,∠GCB=∠PCD. ∵ ∠GCP=60°, ∴ ∠BCD=60°, ∴ △GCP和△BCD都是等边三角形。 ∵ ∠AGC=120°, ∠CGP=60°. ∴ A、G、P三点一线。 ∵ ∠CPD=120°, ∠CPG=60°. ∴ G、P、D三点一线。 ∴ AG、GP、PD三条线段同在一条直线上。 ∵ GA+GC+GB=GA+GP+PD=AD. ∴ G点是等腰三角形内到三个顶点的距离之和最小的那一点 变式练习>>> 1．如图，是边长为1的等边内的任意一点，求的取值范围. 解：将绕点顺时针旋转60°得到， 易知为等边三角形. 从而 （两点之间线段最短），从而. 过作的平行线分别交于点， 易知. 因为在和中， ①， ②。 又，所以③. ①+②+③可得 ， 即.综上，的取值范围为. 例题2. 已知正方形ABCD内一动点E到A、B、C三点的距离之和的最小值为，求正方形的边长． 解 如图2，连接AC，把△AEC绕点C顺时针旋转60°，得到△GFC，连接EF、BG、AG， 可知△EFC、△AGC都是等边三角形，则EF=CE．又FG=AE， ∴AE+BE+CE = BE+EF+FG． ∵ 点B、点G为定点（G为点A绕C点顺时针旋转60°所得）． ∴ 线段BG即为点E到A、B、C三点的距离之和的最小值，此时E、F两点都在BG上． 设正方形的边长为，那么 BO=CO=，GC=, GO=． ∴ BG=BO+GO =+． ∵ 点E到A、B、C三点的距离之和的最小值为． ∴ +=，解得=2． 注 本题旋转△AEB、△BEC也都可以，但都必须绕着定点旋转，读者不妨一试． 变式练习>>> 2．若P为锐角△ABC的费马点，且∠ABC=60°，PA=3，PC=4, 求PB的值. 例题3. 如图，矩形ABCD是一个长为1000米，宽为600米的货场，A、D是入口，现拟在货场内建一个收费站P，在铁路线BC段上建一个发货站台H，设铺设公路AP、DP以及PH之长度和为l，求l的最小值． 【解答】，线段A1E为最短． 变式练习>>> 3．如图，某货运场为一个矩形场地ABCD，其中AB＝500米，AD＝800米，顶点A，D为两个出口，现在想在货运广场内建一个货物堆放平台P，在BC边上（含B，C两点）开一个货物入口M，并修建三条专用车道PA，PD，PM．若修建每米专用车道的费用为10000元，当M，P建在何处时，修建专用车道的费用最少？最少费用为多少？（结果保留整数） 连接AM，DM，将△ADP绕点A逆时针旋转60°，得△AP′D′， 由（2）知，当M，P，P′，D′在同一条直线上时，AP+PM+DP最小，最小值为D′N， ∵M在BC上， ∴当D′M⊥BC时，D′M取最小值， 设D′M交AD于E， ∵△ADD′是等边三角形， ∴EM＝AB＝500， ∴BM＝400，PM＝EM﹣PE＝500﹣， ∴D′E＝AD＝400， ∴D′M＝400+500， ∴最少费用为10000×（400+500）＝1000000（4+5）元； ∴M建在BC中点（BM＝400米）处，点P在过M且垂直于BC的直线上，且在M上方（500﹣）米处，最少费用为1000000 ... ...