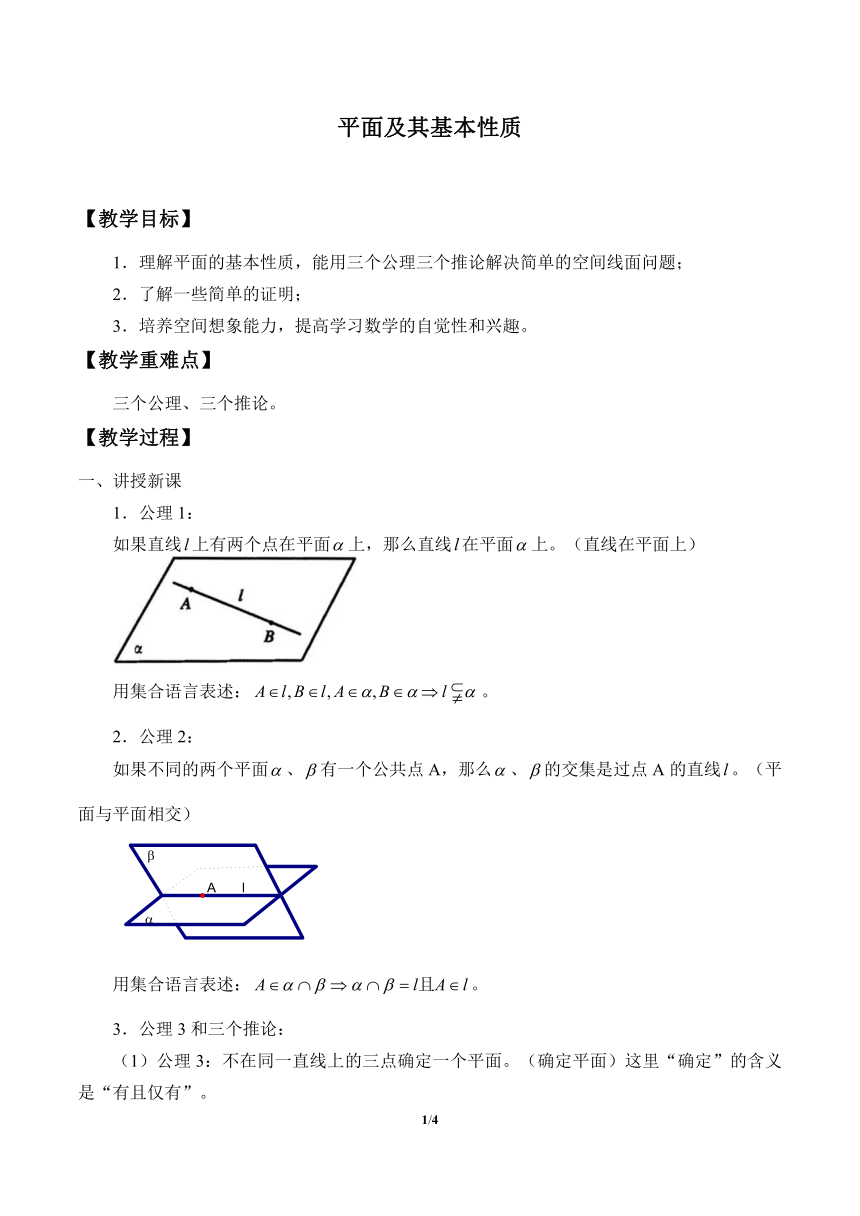
平面及其基本性质 【教学目标】 1.理解平面的基本性质,能用三个公理三个推论解决简单的空间线面问题; 2.了解一些简单的证明; 3.培养空间想象能力,提高学习数学的自觉性和兴趣。 【教学重难点】 三个公理、三个推论。 【教学过程】 一、讲授新课 1.公理1: 如果直线上有两个点在平面上,那么直线在平面上。(直线在平面上) 用集合语言表述:。 2.公理2: 如果不同的两个平面、有一个公共点A,那么、的交集是过点A的直线。(平面与平面相交) 用集合语言表述:。 3.公理3和三个推论: (1)公理3:不在同一直线上的三点确定一个平面。(确定平面)这里“确定”的含义是“有且仅有”。 用集合语言表述:A,B,C不共线=>A,B,C确定一个平面。 (2)推论1:一条直线和直线外的一点确定一个平面。 证明: 设A是直线外的一点,在直线上任取两点B和C,由公理3可知A,B和C三点能确定平面。又因为点,所以由公理1可知B,C所在直线,即平面是由直线和点A确定的平面。 用集合语言表述:。 (3)推论2:两条相交的直线确定一个平面。 用集合语言表述:。 (4)推论3:两条平行的直线确定一个平面。 用集合语言表述:。 4.例题解析: 例1:如图,正方体中,E,F分别是的中点,问:直线EF和BC是否相交?如果相交,交点在那个平面内? 解:; 又,则直线EF和BC共面; 。 设直线EF和BC相交于点p,则p在直线BC上,即点P在平面ABCD上。 说明:利用公理1确定直线在平面内。 例2:如图,若,求证:直线C必过点P。 解:。 结论:三个平面两两相交得到三条交线,若其中两条交于一点,另一条必过此公共点。 例3:空间三个点能确定几个平面?空间四个点能确定几个平面? 解:三点共线有无数多个平面;三点不共线可以确定一个平面。所以三点可以确定一个或无数个平面。 四点共线有无数个平面;有三点共线可确定一个平面;任意三点不共线能确定1个或3个平面。所以四点可以确定1个或3个或无数个平面。 说明:公理3的简单应用。 例4:空间三条直线相交于一点,可以确定几个平面?空间四条直线相交于一点,可以确定几个平面? 解:三条直线相交于一点可以确定1个或3个平面; 四条直线相交于一点可以确定1个、4个或6个平面。 说明:推论2的简单应用。 例5:如图,AB//CD,,求作BC与平面的交点。 解:连接EF和BC,交点即为所求BC与平面的交点。(公理3和公理2) 说明:推论3的简单应用。 三、课堂小结 1.公理1:确定直线在平面内; 2.公理2:平面与平面相交于一直线; 3.公理3和三个推论确定平面的条件。 α 1/1
~~ 您好,已阅读到文档的结尾了 ~~