湘教版数学七年级下册 5.1.2 轴对称变换同步练习 （word版含答案）

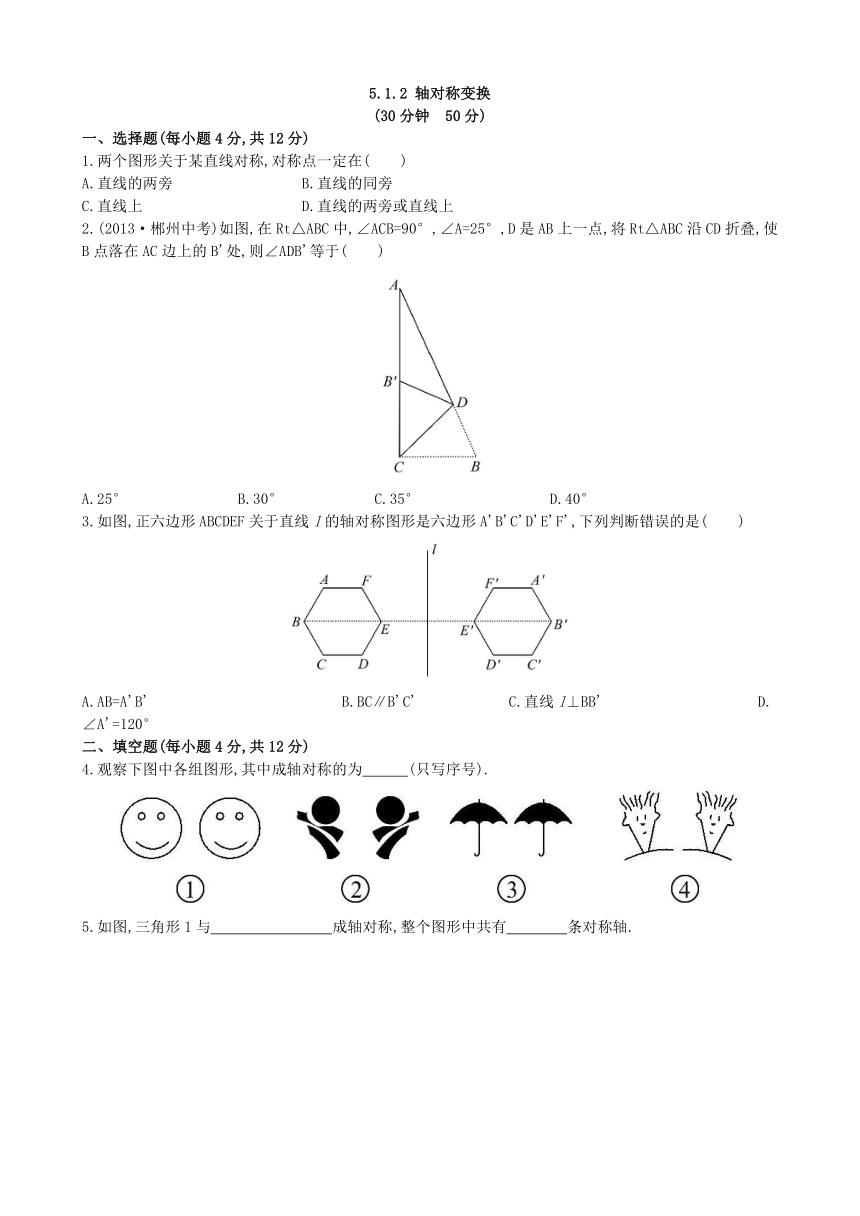
5.1.2 轴对称变换 (30分钟　50分) 一、选择题(每小题4分,共12分) 1.两个图形关于某直线对称,对称点一定在(　　) A.直线的两旁 B.直线的同旁 C.直线上 D.直线的两旁或直线上 2.(2013·郴州中考)如图,在Rt△ABC中,∠ACB=90°,∠A=25°,D是AB上一点,将Rt△ABC沿CD折叠,使B点落在AC边上的B'处,则∠ADB'等于(　　) A.25° B.30° C.35° D.40° 3.如图,正六边形ABCDEF关于直线l的轴对称图形是六边形A'B'C'D'E'F',下列判断错误的是(　　) A.AB=A'B' B.BC∥B'C' C.直线l⊥BB' D.∠A'=120° 二、填空题(每小题4分,共12分) 4.观察下图中各组图形,其中成轴对称的为　　　(只写序号). 5.如图,三角形1与　　　　　　　　成轴对称,整个图形中共有　　　　条对称轴. 6.如图,将一张长方形纸片ABCD沿EF折叠,使顶点C,D分别落在点C',D'处,C'E交AF于点G.若∠CEF=70°,则∠GFD'=　　　　°. 三、解答题(共26分) 7.(8分)辨别下列图形是不是轴对称图形或成轴对称,并说明理由. 8.(8分)如图,在10×10的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上). (1)在图中作出△ABC关于直线l对称的△A1B1C1.(要求:A与A1,B与B1,C与C1相对应) (2)在(1)题的结果下,连接BB1,CC1,求四边形BB1C1C的面积. 【拓展延伸】 9.(10分)在3×3的正方形格点图中,有格点△ABC和△DEF,且△ABC和△DEF关于某直线成轴对称,请在下面的备用图中画出所有这样的△DEF. 参考答案 1.D 【解析】由成轴对称的性质知,若图形的点在直线上,则其对称点在直线上;若图形的点不在直线上,则在直线的两旁. 2.D 【解析】∠B=65°,根据轴对称的性质可知,∠CB'D=∠B=65°,所以∠ADB'=∠CB'D-∠A=65°-25°=40°. 3.B 【解析】由图形可知:A.点A和的对称点是点A'和B',所以AB=A'B'.故A是正确的; B.点B,C,D,E的对称点是点B',C',D'和E',所以根据正六边形的性质可得到BC∥D'E',DE∥B'C'.故B是错误的. C.点B,E的对称点分别是点B',E',所以BB'⊥直线l.故C是正确的. D.正六边形ABCDEF关于直线l的轴对称图形是六边形A'B'C'D'E'F'.所以六边形A'B'C'D'E'F'也是正六边形,则∠A'=120°.故D是正确的. 4.①②④ 【解析】③中的伞把不对称,故填①②④. 5.三角形2、三角形4　2 【解析】根据轴对称的性质可得三角形1与三角形2、三角形4都分别成轴对称,整个图形为轴对称图形,有2条对称轴. 6.40 【解析】因为四边形ABCD是长方形,所以AD∥BC,所以∠GFE=∠CEF=70°,∠CEF+∠EFD=180°.所以∠EFD=110°.由折叠可知∠EFD'=∠EFD=110°,故∠GFD'=∠EFD'-∠GFE=110°-70°=40°. 7.解：辨别的标准只有一个,即“轴对称图形”和“关于直线成轴对称”的定义,也就是看沿某条直线翻折过去能否重合.找到这样的直线,才能下肯定的结论. 图形①可以看成由两部分组成,一部分是完整的圆,另一部分是具有相同圆心的两个圆的大半部分,把它们沿过两个圆心的直线翻折就能重合,所以①是轴对称图形. 将图形②适当进行翻折,眼睛不能重合,所以这不是轴对称图形. 图形③由于两个图形需要平移后再翻折才能重合,所以它们不是关于直线成轴对称的. 图形④是由三个图形组成的,但它毕竟是作为一个整体出现的.这个整体符合轴对称图形的定义,是轴对称图形. 8.解：(1)如图,△A1B1C1是△ABC关于直线l的对称图形. (2)由图得四边形BB1C1C是等腰梯形,BB1=4,CC1=2,高是4. 所以=×(BB1+CC1)×4=×(4+2)×4=12. 9.解:如图所示: ... ...