北京课改版数学八年级上册同步课时练习：12.12　勾股定理的逆定理(word版含答案)

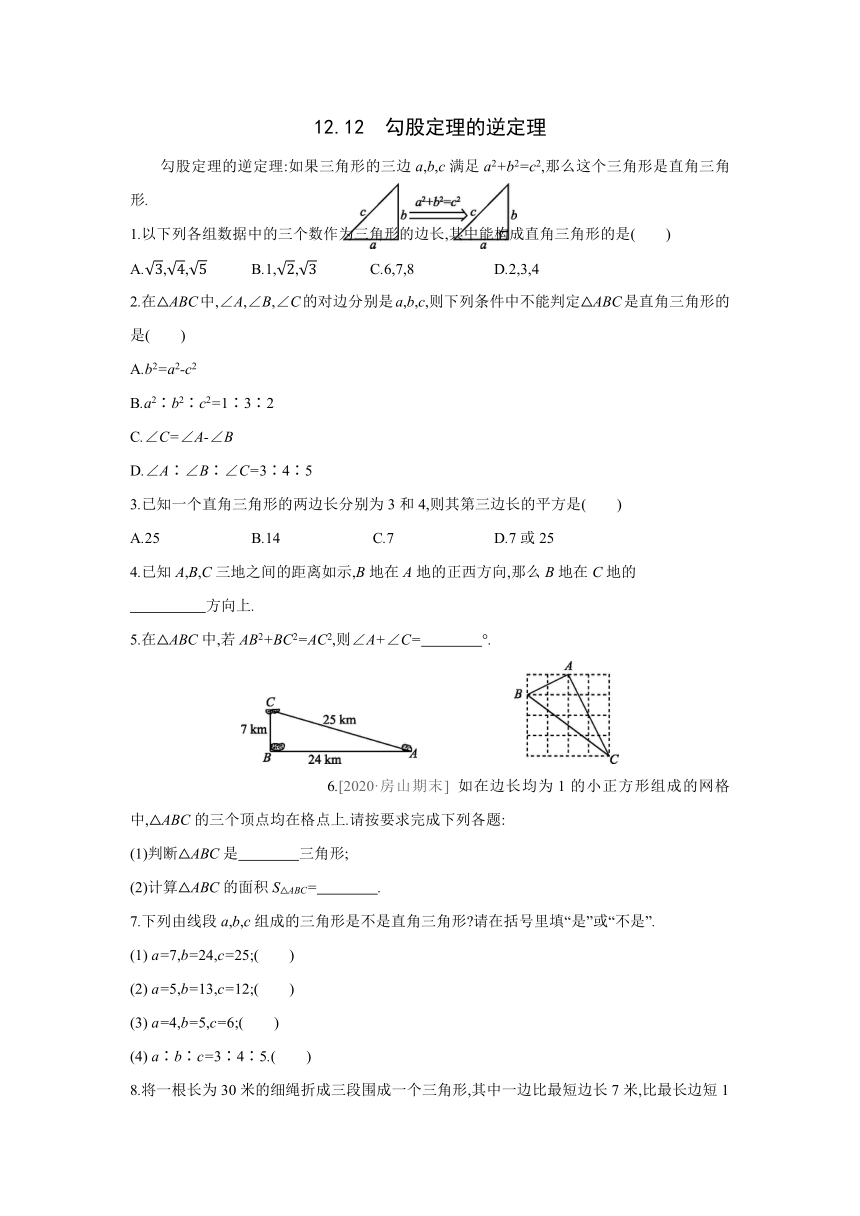
12.12　勾股定理的逆定理 勾股定理的逆定理:如果三角形的三边a,b,c满足a2+b2=c2,那么这个三角形是直角三角形. 1.以下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是(　　) A.,, B.1,, C.6,7,8 D.2,3,4 2.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,则下列条件中不能判定△ABC是直角三角形的是(　　) A.b2=a2-c2 B.a2∶b2∶c2=1∶3∶2 C.∠C=∠A-∠B D.∠A∶∠B∶∠C=3∶4∶5 3.已知一个直角三角形的两边长分别为3和4,则其第三边长的平方是(　　) A.25 B.14 C.7 D.7或25 4.已知A,B,C三地之间的距离如示,B地在A地的正西方向,那么B地在C地的 　　　　　方向上.　 5.在△ABC中,若AB2+BC2=AC2,则∠A+∠C=　　　　°. 6.[2020·房山期末] 如在边长均为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.请按要求完成下列各题: (1)判断△ABC是　　　　三角形; (2)计算△ABC的面积S△ABC=　　　　. 7.下列由线段a,b,c组成的三角形是不是直角三角形 请在括号里填“是”或“不是”. (1) a=7,b=24,c=25;(　　) (2) a=5,b=13,c=12;(　　) (3) a=4,b=5,c=6;(　　) (4) a∶b∶c=3∶4∶5.(　　) 8.将一根长为30米的细绳折成三段围成一个三角形,其中一边比最短边长7米,比最长边短1米,试判断这个三角形的形状,并说明理由. 9.如在△ABC中,AB=13 cm,AC=24 cm,中线BD=5 cm. 求证:△ABC是等腰三角形. 10.已知△ABC的三边长分别是a,b,c,且满足a2+b2+c2+50=6a+8b+10c,试判断△ABC是不是直角三角形. 11.能够成为直角三角形三条边长的三个正整数,称为勾股数.对于任意两个正整数m,n(m>n),下列各组中的三个数为勾股数的一组是(　　) A.m2+mn,m2-1,2mn B.m2-n2,2mn,m2+n2 C.m+n,m-n,2mn D.n2-1,n2+mn,2mn 12.如示,每个小方格都是边长为1的正方形,A,B是方格纸的两个格点(即正方形的顶点),在这个5×5的方格纸中,找出格点C,使△ABC是面积为1的直角三角形,这样的格点C有　　　　个. 13.[2020·燕山期末] 如四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5. (1)求证:AC⊥CD; (2)求四边形ABCD的面积. 14.已知:如在△ABC中,CD是AB边上的高,且CD2=AD·BD. 求证:△ABC是直角三角形. 15.[2020·密云期末] 如△ABC中,AB的垂直平分线l交AB于点E,交AC于点D,AD=5,DC=3,BC=4. (1)求证:△ABC是直角三角形; (2)求AB的长. 16.如,点C,D把线段AB分割成AC,CD和DB三条线段,若以AC,CD,DB为边的三角形是一个直角三角形,则称点C,D是线段AB的勾股分割点. (1)如果点M,N是线段AB的勾股分割点,且AM=3,MN=4,那么NB的长为　　　　; (2)如②,点M,N在线段AB上,且AM∶MN∶NB=1∶1∶,CM=AM,NC=NB,则∠ACB的度数为　　　　; (3)如③,点M,N是线段AB的勾股分割点,其中MN为最长线段,以AM,MN,NB为三边构造Rt△MCN,使CM=AM,NC=NB,连接AC,BC.依题意画出Rt△MCN,并直接写出∠ACB的度数. 答案 1.B 2.D　 A选项满足b2+c2=a2,B选项满足b2=a2+c2,因此都能判定△ABC是直角三角形;C选项可推出∠A=90°,能判定△ABC是直角三角形;由D选项求出的△ABC三个角的度数分别是45°,60°,75°,故它不是直角三角形. 3.D 4.正南　 因为BC=7 km,AB=24 km,AC=25 km,72+242=252,所以BC2+AB2=AC2, 所以△ABC为直角三角形,即∠CBA=90°, 即B地在C地的正南方向上. [点评] 求出∠CBA的度数后就可判断B地在C地的什么方向上. 5.90 6.(1)直角　(2)5 7.(1)是　(2)是　(3)不是　(4)是 (1)∵72 +242 =625,252 =625, ∴72 +242 =252. ∴这个三角形是直角三角形. (2)∵52 +122 =169,132 =169, ∴52 +122 =132. ∴这个三角形是直角三角形. (3)∵42 +52 =41,62 =36, ∴42 +52 ≠62. ∴这个三角形不是直角三角形. (4)设三角形的三边长分别为3k,4k,5k(k>0). ∵(3k)2 + (4k)2 =25k2,(5k)2 =25k2, ∴(3k)2 +(4k)2=(5k)2. ∴ ... ...