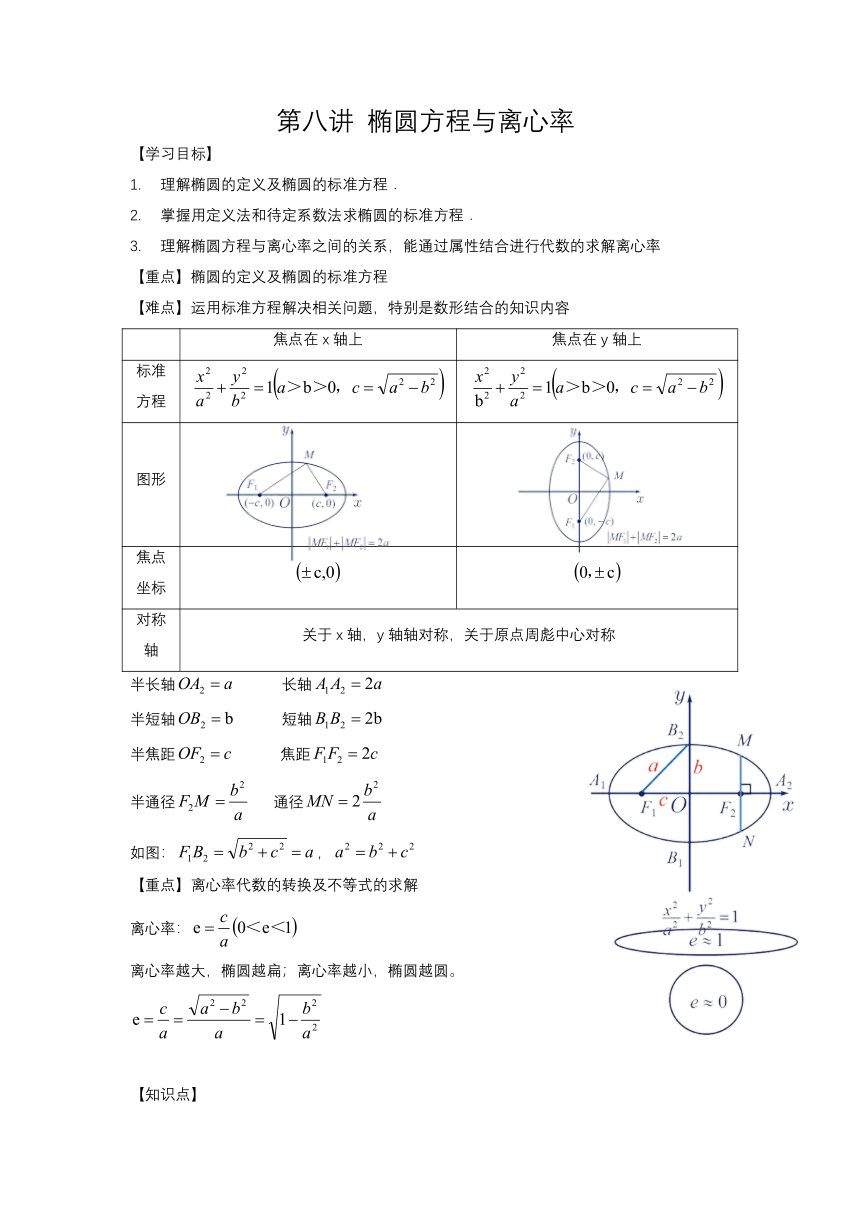
第八讲 椭圆方程与离心率 【学习目标】 理解椭圆的定义及椭圆的标准方程. 掌握用定义法和待定系数法求椭圆的标准方程. 理解椭圆方程与离心率之间的关系,能通过属性结合进行代数的求解离心率 【重点】椭圆的定义及椭圆的标准方程 【难点】运用标准方程解决相关问题,特别是数形结合的知识内容 焦点在x轴上 焦点在y轴上 标准方程 图形 焦点坐标 对称轴 关于x轴,y轴轴对称,关于原点周彪中心对称 半长轴 长轴 半短轴 短轴 半焦距 焦距 半通径 通径 如图:, 【重点】离心率代数的转换及不等式的求解 离心率: 离心率越大,椭圆越扁;离心率越小,椭圆越圆。 【知识点】 椭圆的定义 椭圆定义的应用 椭圆的标准方程 椭圆方程与离心率 【知识点】椭圆的定义 【例1】设P是椭圆上的点.若是椭圆的两个焦点,则等于( ) A.4 B.5 C.8 D.10 【课堂练习】 1、若椭圆上一点到其焦点的距离为6,则到另一焦点的距离为( ) A.4 B.194 C.94 D.14 【知识点】椭圆定义的运用 【例1】(2019福建高二期末)如果表示焦点在轴上的椭圆,那么实数的取值范围是( ) B. C. D. 【例2】过椭圆的一个焦点,且垂直于轴的直线被此椭圆截得的弦长为 【例3】直线被椭圆截得的弦长是( ) A. B. C. D. 【例4】已知点分别是椭圆的左、右焦点,点在此椭圆上,则的周长等于( ) A.20 B.16 C.18 D.14 【课堂练习】 1、如果方程表示焦点在x轴上的椭圆,则实数a的取值范围是( ) A. B. C.或 D.或 2、已知椭圆与直线交于,两点,且,则实数的值为( ) A. B. C. D. 3、已知P是椭圆上的一点,F1,F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是_____. 【知识点】椭圆的标准方程 【例1】焦点在轴上,长轴长为,焦距为的椭圆标准方程; 【例2】与椭圆具有相同的离心率且过点的椭圆的标准方程 【课堂练习】 1、已知椭圆的上顶点为,右顶点为,若过原点作的垂线交椭圆的右准线于点,点到轴的距离为,则此椭圆的离心率为( ) A. B. C. D. 2、(安徽模拟)已知椭圆的左,右焦点分别为F1,F2,若在直线上x=2a存在点P使得线段PF1的垂直平分线过点F2,则离心率范围是 第八讲 椭圆方程与离心率 【学习目标】 理解椭圆的定义及椭圆的标准方程. 掌握用定义法和待定系数法求椭圆的标准方程. 理解椭圆方程与离心率之间的关系,能通过属性结合进行代数的求解离心率 【重点】椭圆的定义及椭圆的标准方程 【难点】运用标准方程解决相关问题,特别是数形结合的知识内容 焦点在x轴上 焦点在y轴上 标准方程 图形 焦点坐标 对称轴 关于x轴,y轴轴对称,关于原点周彪中心对称 半长轴 长轴 半短轴 短轴 半焦距 焦距 半通径 通径 如图:, 【重点】离心率代数的转换及不等式的求解 离心率: 离心率越大,椭圆越扁;离心率越小,椭圆越圆。 【知识点】 椭圆的定义 椭圆定义的应用 椭圆的标准方程 椭圆方程与离心率 【知识点】椭圆的定义 【例1】设P是椭圆上的点.若是椭圆的两个焦点,则等于( ) A.4 B.5 C.8 D.10 【答案】D 【分析】有椭圆的定义可得,椭圆上的点到焦点的距离之和是定长。 【详解】因为椭圆的方程为,所以a2=25,由椭圆的的定义知 【课堂练习】 1、若椭圆上一点到其焦点的距离为6,则到另一焦点的距离为( ) A.4 B.194 C.94 D.14 【答案】D 【分析】由椭圆的定义可得,椭圆上的点到焦点的距离之和是定长。 【详解】依题意,且 【知识点】椭圆定义的运用 【例1】(2019福建高二期末)如果表示焦点在轴上的椭圆,那么实数的取值范围是( ) B. C. D. 【答案】A 【分析】利用椭圆的定义,化简为标准方程,根据椭圆焦点所在轴的位置判断对应的a和b的大小。 【详解】 转化为椭圆的标准方程,得,因为表示焦点在y轴上的椭圆,所以,解得. ... ...
~~ 您好,已阅读到文档的结尾了 ~~