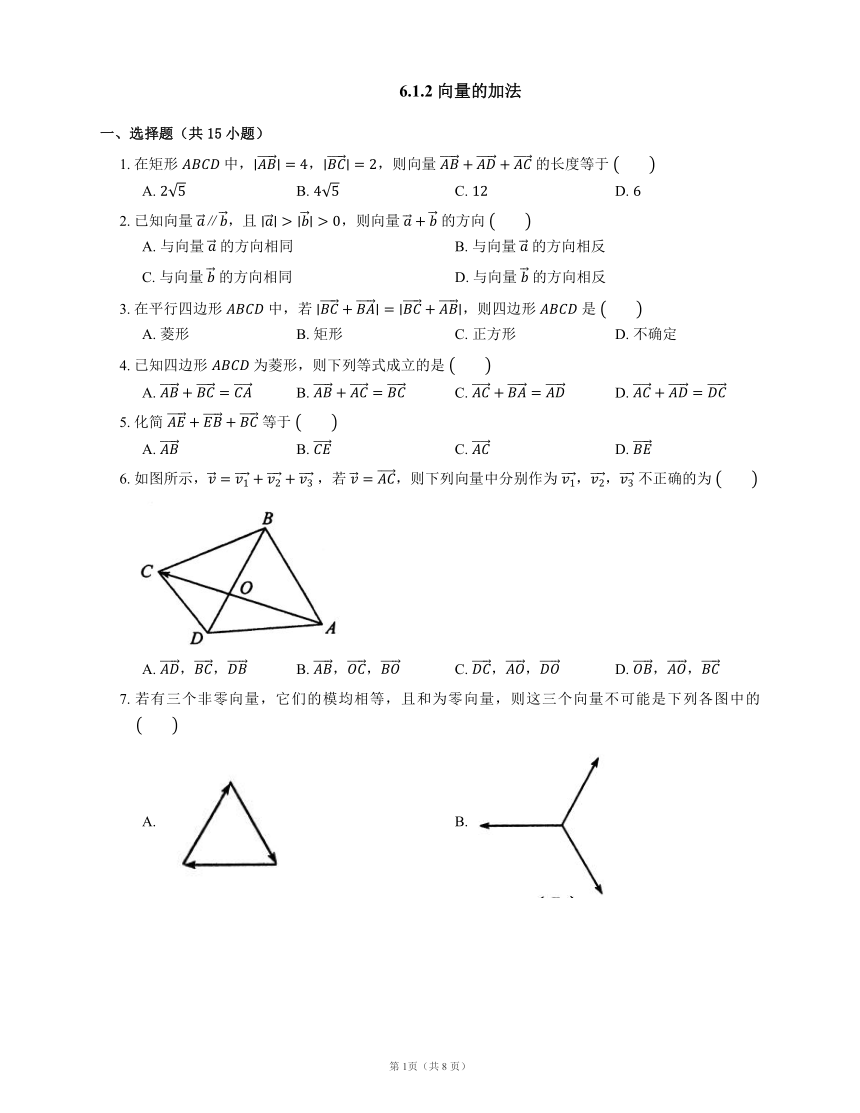
6.1.2 向量的加法 一、选择题(共15小题) 1. 在矩形 中,,,则向量 的长度等于 A. B. C. D. 2. 已知向量 ,且 ,则向量 的方向 A. 与向量 的方向相同 B. 与向量 的方向相反 C. 与向量 的方向相同 D. 与向量 的方向相反 3. 在平行四边形 中,若 ,则四边形 是 A. 菱形 B. 矩形 C. 正方形 D. 不确定 4. 已知四边形 为菱形,则下列等式成立的是 A. B. C. D. 5. 化简 等于 A. B. C. D. 6. 如图所示, ,若 ,则下列向量中分别作为 ,, 不正确的为 A. ,, B. ,, C. ,, D. ,, 7. 若有三个非零向量,它们的模均相等,且和为零向量,则这三个向量不可能是下列各图中的 A. B. C. D. 8. 当 ,且 , 不共线时, 与 的关系是 A. 平行 B. 相等 C. 相交但不垂直 D. 垂直 9. 下列各式不正确的是 A. 若 同向,则 B. 若 不共线,则 C. 若 反向,则 D. 若 不共线,则 10. 已知圆 的半径为 ,,,, 为该圆上四个点,且 ,则 的面积最大值为 A. B. C. D. 11. 四边形 中, 且 ,则四边形 为 A. 平行四边形 B. 菱形 C. 矩形 D. 正方形 12. 设 ,,, 是平面上给定的 个不同点,则使 成立的点 的个数为 . A. B. C. D. 13. 设 为平行四边形 对角线的交点, 为平行四边形 所在平面内任意一点,则下列等于 的是 A. B. C. D. 14. 已知 是四边形 内一点,若 ,则下列结论正确的是 A. 四边形 为正方形,点 是正方形 的中心 B. 四边形 为一般四边形,点 是四边形 的对角线的交点 C. 四边形 为一般四边形,点 是四边形 的外接圆的圆心 D. 四边形 为一般四边形,点 是四边形 的对边中点连线的交点 15. 已知 的三个顶点 ,, 及平面内一点 满足 ,则点 与 的关系为 A. 在 内部 B. 在 外部 C. 在边 所在直线上 D. 是边 的一个三等分点 二、填空题(共5小题) 16. 化简 的结果为 . 17. 在平面上 ,,.若 ,则 的取值范围为 . 18. 已知下列四个命题: ①对任意两向量 ,,均有 ; ②若 ,则 是线段 的中点; ③在四边形中,若 ,则 为平行四边形; ④若 中,,则 . 其中正确命题的序号是 . 19. 若 为 的外心,且 ,则 . 20. 如图,在边长为 的正方形ABCD中,设 ,则 . 三、解答题(共6小题) 21. 如图,已知向量 ,,求作向量 . 22. 已知正方形 的边长等于 ,,,,试作向量: (1); (2) . 23. 在四边形 中,对角线 , 交于点 ,且 ,,.求 与 的值. 24. 一艘船以 的速度向垂直于对岸的方向行驶,该船实际的航行方向与水流方向成 角,求水流速度和船的实际速度. 25. 如图,已知点 是 的重心.求证:. 26. 设点 是线段 中点,点 在直线 外,且 ,,求 . 答案 1. B 2. A 【解析】据向量加法的几何意义, 的方向应与 的方向一致. 3. B 【解析】由图知 . 又 ,所以 ,所以四边形 为矩形. 4. C 【解析】在菱形 中,. 5. C 【解析】. 6. C 7. D 8. D 9. A 10. B 【解析】如图所示, 由 知, 为平行四边形, 又 ,,, 四点共圆, 所以 为矩形,即 为圆的直径, 所以当 时, 的面积取得最大值为 . 11. C 【解析】因为四边形 中,,所以四边形 是平行四边形.因为 ,所以 ,即对角线相等,所以平行四边形 是矩形. 12. B 13. D 【解析】由已知,得 ,,,, 而 ,, 所以 . 14. D 15. D 16. 17. 【解析】因为四边形 是矩形,不难得出:, , 所以 的取值范围为 . 18. ②③ 【解析】若两向量 , 方向相反,则①不对;由向量平行四边形法则可知②对;③中向量等式化简后为 ,说明 平行 且 等于 ,所以③对;由向量平行四边形法则可知④不对. 19. 【解析】因为 ,则四边形 是平行四边形. 又 为 的外心,所以 ,因此 . 20. 【解析】先利用向量加减运算律及有关知识将 化简为用有向线段表示的向量,便于求模. ,过 作 (图),则 . ... ...
~~ 您好,已阅读到文档的结尾了 ~~