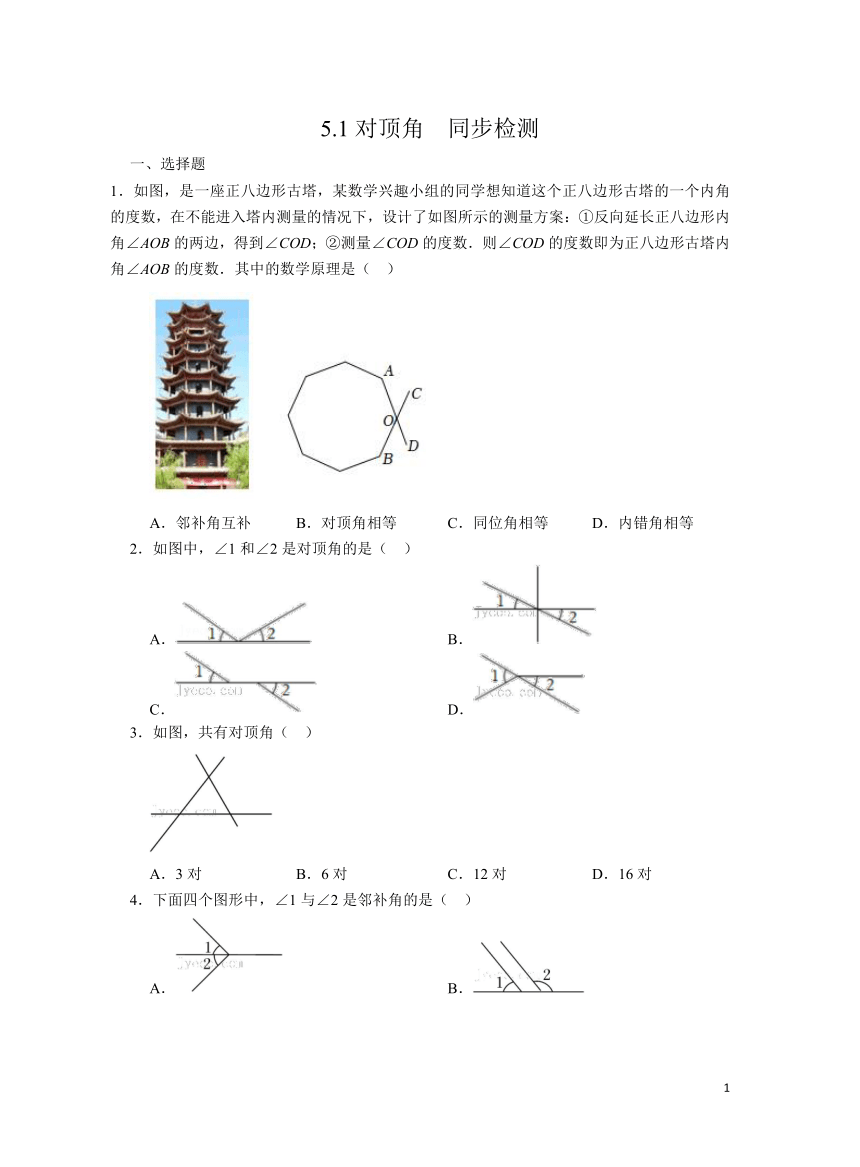
5.1对顶角 同步检测 选择题 1.如图,是一座正八边形古塔,某数学兴趣小组的同学想知道这个正八边形古塔的一个内角的度数,在不能进入塔内测量的情况下,设计了如图所示的测量方案:①反向延长正八边形内角∠AOB的两边,得到∠COD;②测量∠COD的度数.则∠COD的度数即为正八边形古塔内角∠AOB的度数.其中的数学原理是( ) A.邻补角互补 B.对顶角相等 C.同位角相等 D.内错角相等 2.如图中,∠1和∠2是对顶角的是( ) A. B. C. D. 3.如图,共有对顶角( ) A.3对 B.6对 C.12对 D.16对 4.下面四个图形中,∠1与∠2是邻补角的是( ) A. B. C. D. 5.若∠A=54°,则∠A的邻补角是( ) A.36° B.126° C.46° D.136° 6.如图,两条直线交于点O,若∠1+∠2=80°,则∠3的度数为( ) A.40° B.80° C.100 D.140° 7.如图,三条直线A.B.c相交于一点,则∠1+∠2+∠3等于( ) A.180° B.120° C.90° D.不能确定 8.如图,直线AB,CD相交于点O,若∠AOD减少30°,则∠BOC( ) A.增大30° B.增大150° C.不变 D.减少30° 9.如图,直线AB.CD交于点O,∠2=3∠1,∠BOD=108°,则∠1=( ) A.27° B.36° C.81° D.72° 10.如图,直线AB,CD相交于点O,已知∠BOE=15°,∠AOD=2∠DOE,则∠DOB的度数为( ) A.50° B.56° C.60° D.65° 二、填空题: 11.若∠1和∠2是对顶角,∠1=36°,则∠2的度数是 度. 12.如图,二条直线l1与l2.l3相交于点O,l1与l3夹角为50°,则∠1+∠2= . 13.如图,直线a与b相交,∠1+∠2=240°,∠3= . 14.观察下列各图,寻找对顶角(不含平角).如图1,图中有2条直线相交,则对顶角有 对;如图2,图中有3条直线相交于一点,则对顶角有 对;如图3图中有n条直线相交于一点,则对顶角有 对. 三、解答题: 15.如图,直线AB与CD相交,∠1=30°,求∠2,∠3,∠4的度数. 16.已知两条直线A.b相交,其中∠3=3∠1,求∠2的度数. 17.如图,直线m和l交于O点,已知∠1的补角是它的余角的4倍,求∠2的度数. 18.如图所示,直线a,b,c两两相交,∠1=∠3+12°,∠2=52°,求∠4的度数. 参考答案: 1.B解:∠COD的度数即为∠AOB的度数,其中的数学原理是对顶角相等,故选:B. 2.B解:由对顶角的定义可知,图中的∠1与∠2是对顶角,故选:B. 3.B解:两条直线相交于一点,共有对顶角的对数为2对, 三条直线两两相交,有三个交点,共有对顶角的对数为6对.故选:B. 4.C解:根据邻补角的定义可知, 图中的∠1与∠2是邻补角, 故选:C. 5.B解:∠A=54°,则∠A的邻补角为180°﹣54°=126°, 故选:B. 6.D.解:∵∠1=∠2,∠1+∠2=80°, ∴∠1=40°, ∵∠1+∠3=180°, ∴∠3=180°﹣∠1=140°. 故选:D. 7.A解:如图, ∴∠1+∠2+∠4=180°, ∵对顶角∠3=∠4, ∴∠1+∠2+∠3=180°, 故选:A. 8.解:解:∵∠AOD=∠BOC, ∴∠AOD减少30°时,∠BOC也减少30°, 故选:D. 9.A解:∠BOD=∠AOC=108°, ∵∠AOC=∠1+∠2,∠2=3∠1, ∴4∠1=108°, ∠1=27°, 故选:A. 10.A解:∠BOD=∠AOC=108°, ∵∠AOC=∠1+∠2,∠2=3∠1, ∴4∠1=108°, ∠1=27°, 故选:A. 填空题: 11.解:∵∠1和∠2是对顶角,∠1=36°, ∴∠2=∠1=36°. 故答案为:36. 2.解:根据对顶角相等,得∠1+∠2=180°﹣50°=130°. 故答案为:130° 解:∵∠AOB+∠COD=60°,∠AOB=∠COD, ∴∠AOB=30°, ∵∠AOC+∠AOB=180°, ∴∠AOC=150°, 故答案为:30°. 13.解:∵∠1=∠2,∠1+∠2=240°, ∴∠1=∠2=120°, ∵∠1+∠3=180°, ∴∠3=180°﹣120°=60°. 故答案为:60°. 14.解:当2条直线相交 ... ...
~~ 您好,已阅读到文档的结尾了 ~~