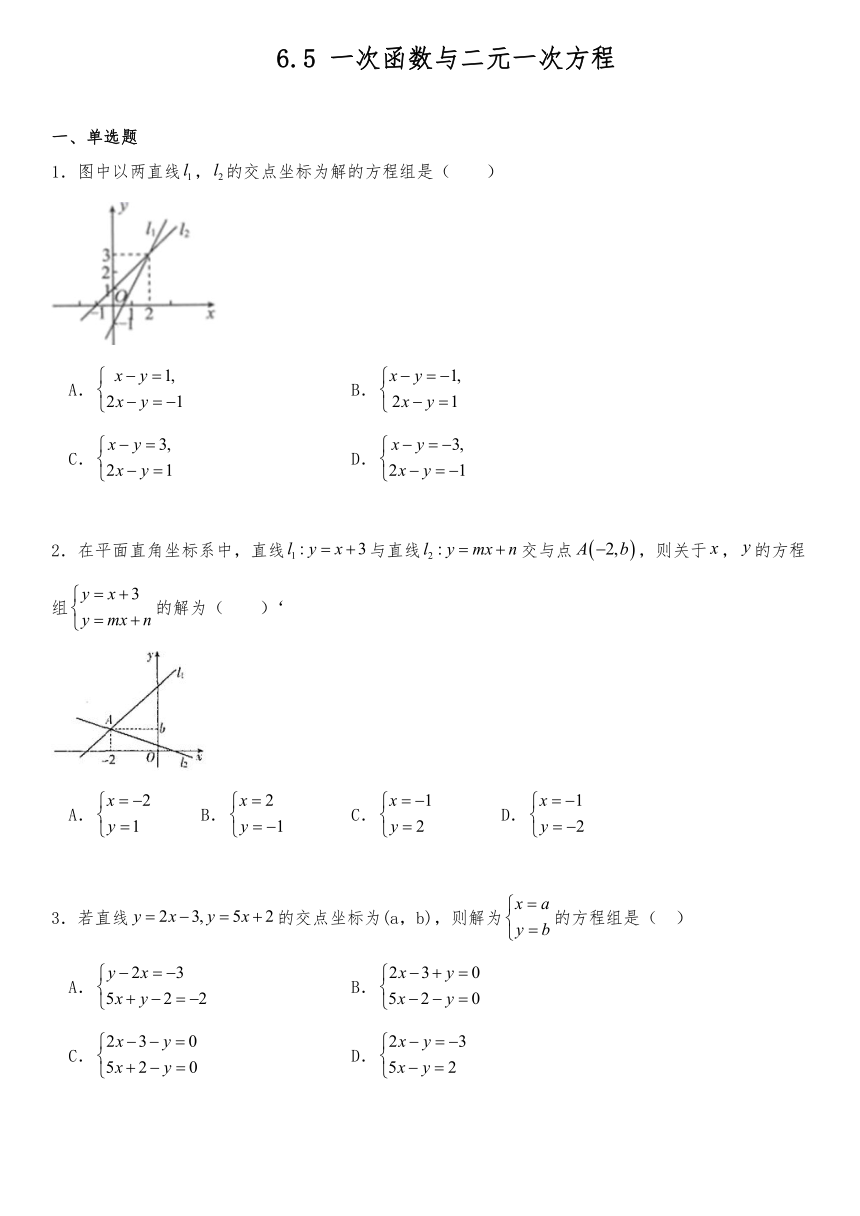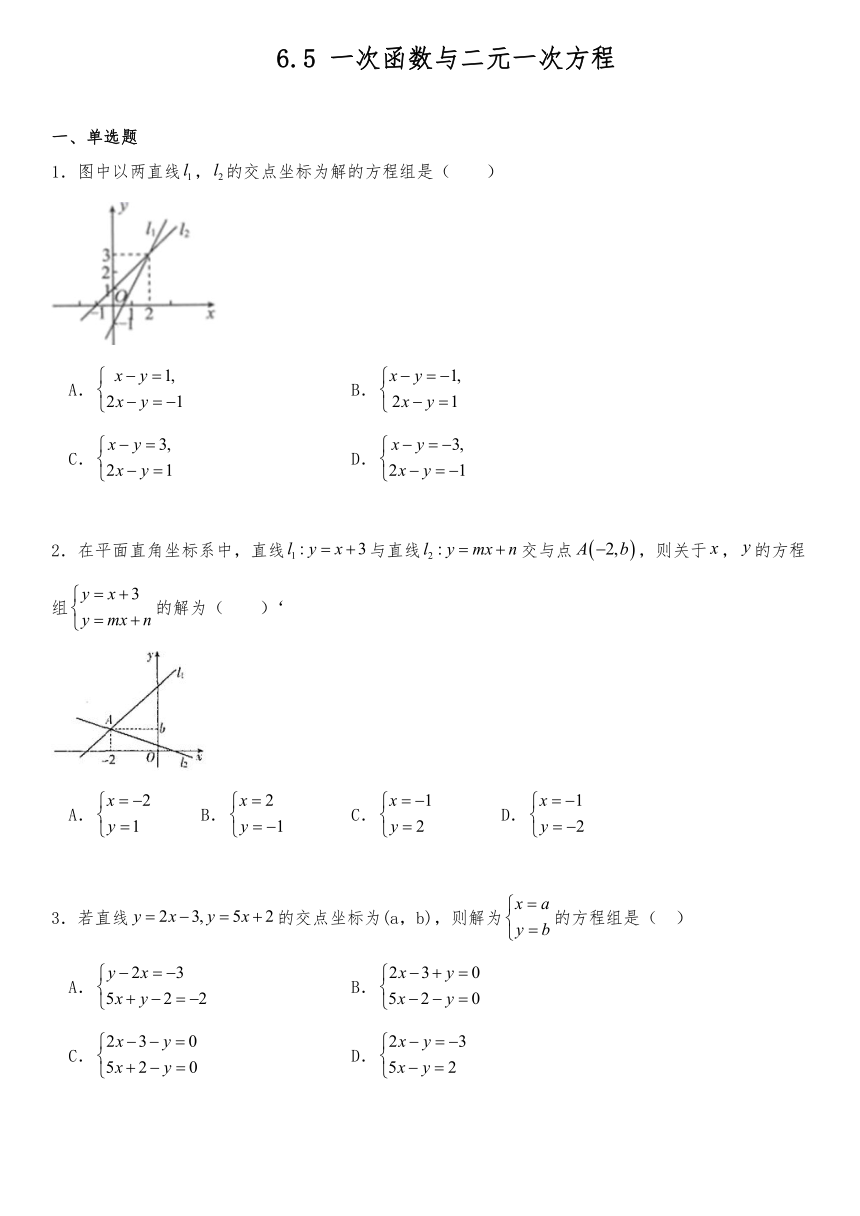
6.5 一次函数与二元一次方程 一、单选题 1.图中以两直线,的交点坐标为解的方程组是( ) A. B. C. D. 2.在平面直角坐标系中,直线与直线交与点,则关于,的方程组的解为( )‘ A. B. C. D. 3.若直线的交点坐标为(a,b),则解为的方程组是( ) A. B. C. D. 4.已知一次函数和一次函数的图象的交点坐标是,据此可知方程组的解为( ) A. B. C. D. 5.函数与的图像相交于点,则( ) A. B. C. D. 6.已知直线与的图象如图,则方程组的解为( ) A. B. C. D. 7.在同一平面直角坐标系中,若一次函数y=-x+1与y=2x+4的图像交于点M,则点M的坐标为( ) A.(-1,-2) B.(-1,2) C.(-2,1) D.(2,1) 8.若两条直线的交点为(2,3),则这两条直线对应的函数解析式可能是( ). A. B. C. D. 9.直线和直线与x轴围成的三角形的面积是( ) A.32 B.64 C.16 D.8 10.如图,若直线y=kx+b与x轴交于点A(-4,0),与y轴正半轴交于B,且△OAB的面积为4,则该直线的解析式为( ) A.y=x+2 B.y=2x+2 C.y=4x+4 D.y=x+4 二、填空题 11.如图,直线与直线交于点,则关于,的二元一次方程组的解为_____. 12.已知方程组的解为,则一次函数y=2x+3与y=ax+c的图象的交点坐标是_____. 13.如图,则方程组的解为_____. 14.如图所示,直线、的交点坐标是_____,它可以看作方程组_____的解. 15.已知关于x,y的方程组的解是,则直线与坐标轴围成的三角形的面积是_____。 三、解答题 16.如图,已知函数和的图象交于点,这两个函数的图象与轴分别交于点、. (1)分别求出这两个函数的解析式; (2)求的面积; (3)根据图象直接写出时,的取值范围. 17.如图,直线的表达式为,且与轴交于点;直线经过,两点.直线,,相交于点. (1)求直线的表达式; (2)求的面积. 18.如图,直线的图象与轴交于点,直线的图象与轴交于点,两者相交于点. (1)方程组的解是 ; (2)当与同时成立时,的取值范围为 ; (3)求的面积; (4)在直线的图象上存在异于点的另一点,使得与的面积相等,请求出点的坐标. 19.点在第一象限,且,点的坐标为,设的面积为. (1)用含的式子表示,写出的取值范围,画出函数的图象; (2)当点的横坐标为5时,的面积是多少? 20.我们曾探究过“以方程的解为坐标的值为横坐标、的值为纵坐标)的点的特性”,了解了二元一次方程的解与其图象上点的坐标的关系. 发现:以方程的解为坐标的所有点组成的图象与一次函数的图象相同,是同一条直线; 结论:一般的,以一个二元一次方程的解为坐标的点组成的图象与相应的一次函数的图象相同,是一条直线. 示例:如图1,我们在画方程的图象时,可以取点和,作出直线. 【解决问题】: (1)请你在图2所给的平面直角坐标系中画出二元一次方程组中的两个二元一次方程的图象(提示:依据“两点确定一条直线”,画出图象即可,无需写过程); (2)观察图象,两条直线的交点坐标为 ,由此你得出这个二元一次方程组的解是 ; 【拓展延伸】: (3)已知二元一次方程的图象经过两点和,试求、的值. (4)在同一平面直角坐标系中,一次函数图象和一次函数的图象,如图3所示, ①请判断和的关系,并说明理由; ②根据图象,请直接判断方程组的解的情况(不需要说明理由). 答案 一、单选题 B.A.C.A.A.B.B.D.C.A. 二、填空题 11.. 12.(-1,1). 13.. 14.(2,2) 15.4. 三、解答题 16. (1)∵将点代入,得,解得. 将点代入,得,解得. 这两个函数的解析式分别为和. (2)∵在中,令,得. . ∵在中,令,得, . . (3)由函数图象可知,当时,. 17.(1)设直线的解析式为, 把A(4,0),B(3,-)代入得, 解得, 所 ... ...
~~ 您好,已阅读到文档的结尾了 ~~