2024湘教版数学七年级下册--专项素养综合全练(七)平行线的性质与判定中的数学思想方法（含解析）

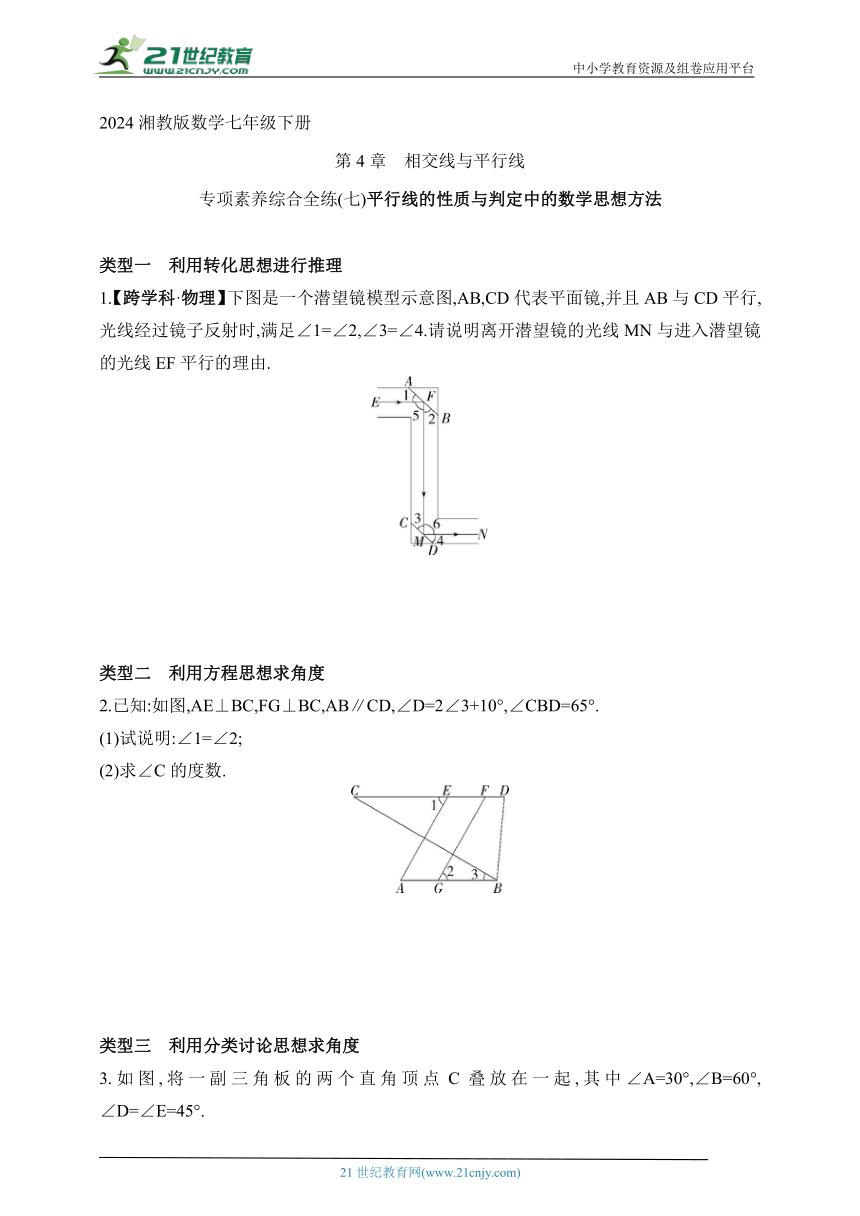
中小学教育资源及组卷应用平台 2024湘教版数学七年级下册 第4章　相交线与平行线 专项素养综合全练(七)平行线的性质与判定中的数学思想方法 　　　　　　　　　　　　　　　　 类型一　利用转化思想进行推理 1.【跨学科·物理】下图是一个潜望镜模型示意图,AB,CD代表平面镜,并且AB与CD平行,光线经过镜子反射时,满足∠1=∠2,∠3=∠4.请说明离开潜望镜的光线MN与进入潜望镜的光线EF平行的理由. 类型二　利用方程思想求角度 2.已知:如图,AE⊥BC,FG⊥BC,AB∥CD,∠D=2∠3+10°,∠CBD=65°. (1)试说明:∠1=∠2; (2)求∠C的度数. 类型三　利用分类讨论思想求角度 3.如图,将一副三角板的两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°, ∠D=∠E=45°. (1)若∠ACE=35°,求∠BCD的度数; (2)试猜想∠ACE与∠BCD的数量关系,并说明理由; (3)若按住三角板ABC不动,绕顶点C转动三角板DCE,试探究∠ACD等于多少度时,CE∥AB,请直接写出结果. 4.已知:如图,点O在∠BAC的一边AC上,过点O的直线MN∥AB,OD平分∠AON,OD⊥OE. (1)若∠A=40°,求∠DOC的度数; (2)猜想∠COE和∠DON的关系,并说明理由; (3)当∠A=　　　　度时,ON分∠AOE成1∶2两部分. 第4章　相交线与平行线 专项素养综合全练(七) 平行线的性质与判定中的数学思想方法 1.解析　∵AB∥CD,∴∠2=∠3,∵∠1=∠2,∠3=∠4,∴∠1=∠2=∠3=∠4,∴∠1+∠2=∠3+∠4,∵∠1+∠2+∠5=180°,∠3+∠4+∠6=180°,∴∠5=∠6.∴MN∥EF. 2.解析　(1)∵AE⊥BC,FG⊥BC,∴AE∥FG,∴∠A=∠2,∵AB∥CD,∴∠A=∠1,∴∠1=∠2. (2)设∠3=x°,则∠D=(2x+10)°,∠ABD=∠3+∠CBD=(x+65)°,∵AB∥CD,∴∠D+∠ABD=180°,∴(2x+10)°+(x+65)°=180°,∴x=35, ∴∠3=35°,∵AB∥CD,∴∠C=∠3=35°. 方法解读　当题目中的数量关系较为复杂时,常设未知数构造方程来解决. 3.解析　(1)∵∠BCA=∠ECD=90°,∠ACE=35°, ∴∠DCA=∠ECD-∠ACE=90°-35°=55°. ∴∠BCD=∠BCA+∠DCA=90°+55°=145°. (2)∠ACE+∠BCD=180°. 理由:∵∠ACE=∠ECD-∠DCA=90°-∠DCA, ∠BCD=∠BCA+∠DCA=90°+∠DCA, ∴∠ACE+∠BCD=90°-∠DCA+90°+∠DCA=180°. (3)120°或60°. 详解:如图,当∠A=∠ACE时,CE∥AB, 此时∠ACD=∠ACE+∠ECD=∠A+∠ECD=30°+90°=120°; 如图,当∠A+∠ACE=180°,即∠ACE=180°-∠A=150°时,CE∥AB, 此时∠ACD=∠ACE-∠DCE=150°-90°=60°. 综上所述,当∠ACD=120°或60°时,CE∥AB. 方法解读　题中图形存在多种情况时,常利用分类讨论思想求解. 4.解析　(1)∵MN∥AB,∠A=40°,∴∠AON=140°, ∵OD平分∠AON,∴∠AOD=∠AON=70°, ∴∠DOC=180°-∠AOD=110°. (2)∠COE+∠DON=90°.理由如下: ∵OD平分∠AON,∴∠DON=∠AOD. ∵OD⊥OE,∴∠EOD=90°,∴∠COE+∠AOD=90°, ∴∠COE+∠DON=90°. (3)当∠EON∶∠AON=1∶2时,∠EON=∠AON, ∵OD平分∠AON,∴∠DON=∠AON=∠EON, ∵∠EON+∠DON=∠DOE=90°,∴∠EON=∠DON=∠DOE=45°, ∴∠AON=2∠EON=90°,∵MN∥AB,∴∠A=180°-∠AON=90°. 当∠EON∶∠AON=2∶1时,∠AON=∠EON, ∵ OD平分∠AON, ∴∠DON=∠AON,∴∠DON=∠EON, ∵∠EON+∠DON=∠EON+∠EON=∠DOE=90°, ∴∠EON=∠DOE=×90°=72°, ∴∠AON=∠EON=36°, ∵MN∥AB,∴∠A=180°-∠AON=144°. 综上所述,当∠A=90°或144°时,ON分∠AOE成1∶2两部分.故答案为90或144. 21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页） 21世纪教育网(www.21cnjy.com) ... ...