高考数学一轮课时规范练习之 解答题专项四　第3课时　翻折问题与探索性问题（含答案）

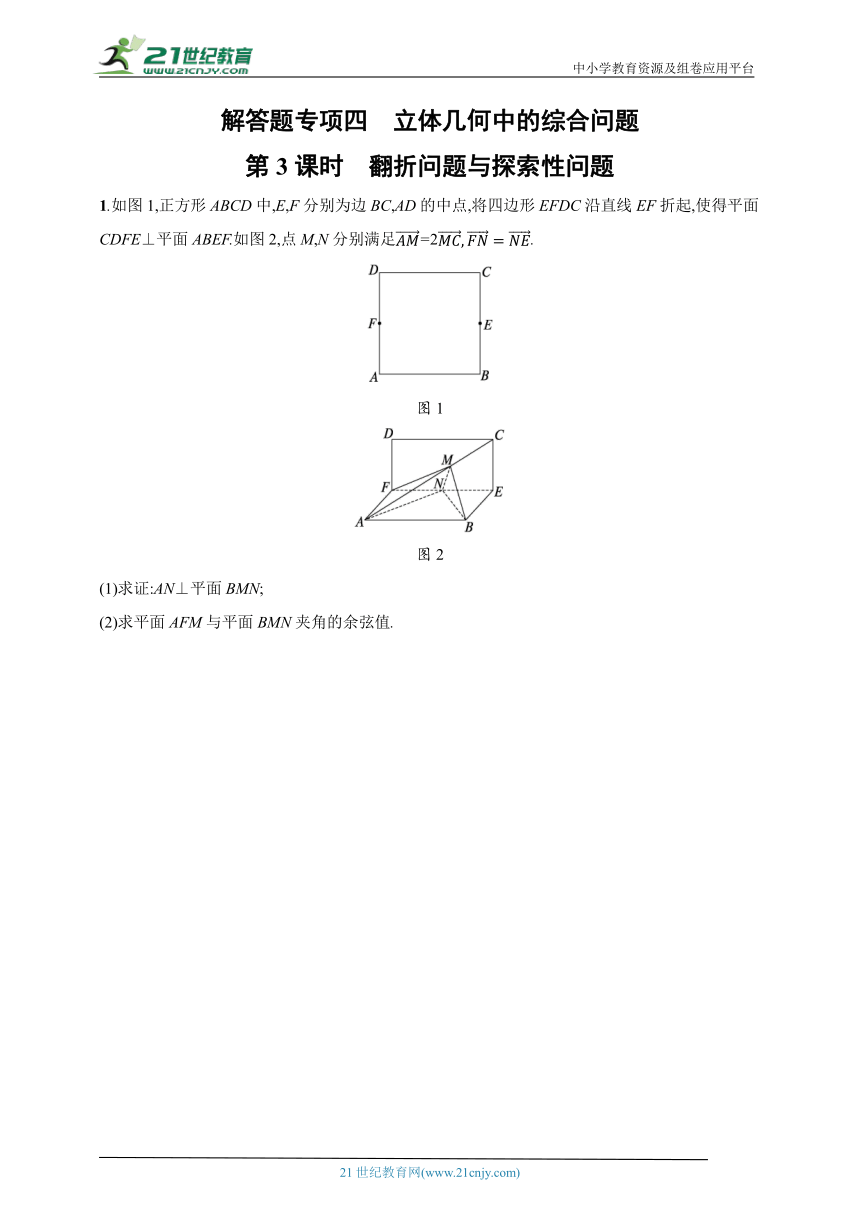
中小学教育资源及组卷应用平台 解答题专项四　立体几何中的综合问题 第3课时　翻折问题与探索性问题 1.如图1,正方形ABCD中,E,F分别为边BC,AD的中点,将四边形EFDC沿直线EF折起,使得平面CDFE⊥平面ABEF.如图2,点M,N分别满足=2. 图1 图2 (1)求证:AN⊥平面BMN; (2)求平面AFM与平面BMN夹角的余弦值. 2.如图,P为圆锥的顶点,O为圆锥底面的圆心,圆锥的底面直径AB=4,母线PH=2,M是PB的中点,四边形OBCH为正方形. (1)设平面POH∩平面PBC=l,证明:l∥BC; (2)设D为OH的中点,N是线段CD上的一个点,当MN与平面PAB所成角最大时,求MN的长. 3.如图,在三棱锥A-BCD中,△ABC是正三角形,平面ABC⊥平面BCD,BD⊥CD,点E,F分别是BC,DC的中点. (1)证明:平面ACD⊥平面AEF; (2)若∠BCD=60°,点G是线段BD上的动点,问:点G运动到何处时,平面AEG与平面ACD所成的锐二面角最小. 4.已知四边形ABCD为平行四边形,E为CD的中点,AB=4,△ADE为等边三角形,将三角形ADE沿AE折起,使点D到达点P的位置,且平面APE⊥平面ABCE. (1)求证:AP⊥BE; (2)试判断在线段PB(不包括P,B点)上是否存在点F,使得平面AEF与平面AEP的夹角为45°.若存在,试确定点F的位置;若不存在,请说明理由. 解答题专项四　立体几何中的综合问题 第3课时　翻折问题与探索性问题 1.如图1,正方形ABCD中,E,F分别为边BC,AD的中点,将四边形EFDC沿直线EF折起,使得平面CDFE⊥平面ABEF.如图2,点M,N分别满足=2. 图1 图2 (1)求证:AN⊥平面BMN; (2)求平面AFM与平面BMN夹角的余弦值. (1)证明:连接AE交BN于点G,连接MG,设AB=2,因为平面CDFE⊥平面ABEF, 平面CDFE∩平面ABEF=EF,CE 平面CDFE,CE⊥EF,所以CE⊥平面ABEF, 因为点N是EF的中点,NE∥AB, 所以AG=2GE. 又因为AM=2MC,所以MG∥CE, 所以MG⊥平面ABEF. 因为AN 平面ABEF,所以MG⊥AN, 又AB=2,AN=NB=,所以AN⊥NB. 因为NB∩MG=G,NB,MG 平面BMN, 所以AN⊥平面BMN. (2)解:因为平面CDFE⊥平面ABEF,平面CDFE∩平面ABEF=FE,DF⊥EF,所以DF⊥平面ABEF. 因为AF 平面ABEF,所以DF⊥AF,所以FA,FE,FD两两垂直, 所以以F为原点,分别以FA,FE,FD所在直线为x,y,z轴建立空间直角坐标系,如图所示, 设AB=2,所以F(0,0,0),A(1,0,0),M,N(0,1,0), 所以=(1,0,0),=, 设平面AFM的一个法向量为n=(x,y,z), 由令y=1,得n=(0,1,-2), 由(1)知平面BMN的一个法向量为=(-1,1,0), 设平面AFM与平面BMN的夹角为θ, 所以cos θ=, 所以平面AFM与平面BMN夹角的余弦值为. 2.如图,P为圆锥的顶点,O为圆锥底面的圆心,圆锥的底面直径AB=4,母线PH=2,M是PB的中点,四边形OBCH为正方形. (1)设平面POH∩平面PBC=l,证明:l∥BC; (2)设D为OH的中点,N是线段CD上的一个点,当MN与平面PAB所成角最大时,求MN的长. (1)证明:因为四边形OBCH为正方形,∴BC∥OH, ∵BC 平面POH,OH 平面POH, ∴BC∥平面POH. ∵BC 平面PBC,平面POH∩平面PBC=l, ∴l∥BC. (2)解:∵圆锥的母线长为2,AB=4,∴OB=2,OP=2, 以O为原点,建立如图所示的空间直角坐标系,则P(0,0,2),B(0,2,0),D(1,0,0),C(2,2,0),M(0,1,1), 设=λ=(λ,2λ,0)(0≤λ≤1),=(1+λ,2λ,0), =(1+λ,2λ-1,-1),=(1,0,0)为平面PAB的一个法向量, 设MN与平面PAB所成的角为θ, 则sin θ= =,令1+λ=t∈[1,2], 则sin θ=, 所以当时,即λ=时,sin θ最大,即θ最大,此时=,-1,所以MN=||=. 3.如图,在三棱锥A-BCD中,△ABC是正三角形,平面ABC⊥平面BCD,BD⊥CD,点E,F分别是BC,DC的中点. (1)证明:平面ACD⊥平面AEF; (2)若∠BCD=60°,点G是线段BD上的动点,问:点G运动到何处时,平面AEG与平面ACD所成的锐二面角最小. (1)证明:因为△ABC是正三角形,点E是BC中点,所以AE⊥BC, 又因为平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,AE 平面ABC,所以AE⊥平面BCD. 因为CD 平面BCD,所以CD⊥AE. 因为点E,F分别是BC,CD的中点, 所以EF∥BD, 因为BD⊥CD ... ...