人教版数学八年级下册 专项练习十 正方形（含答案）

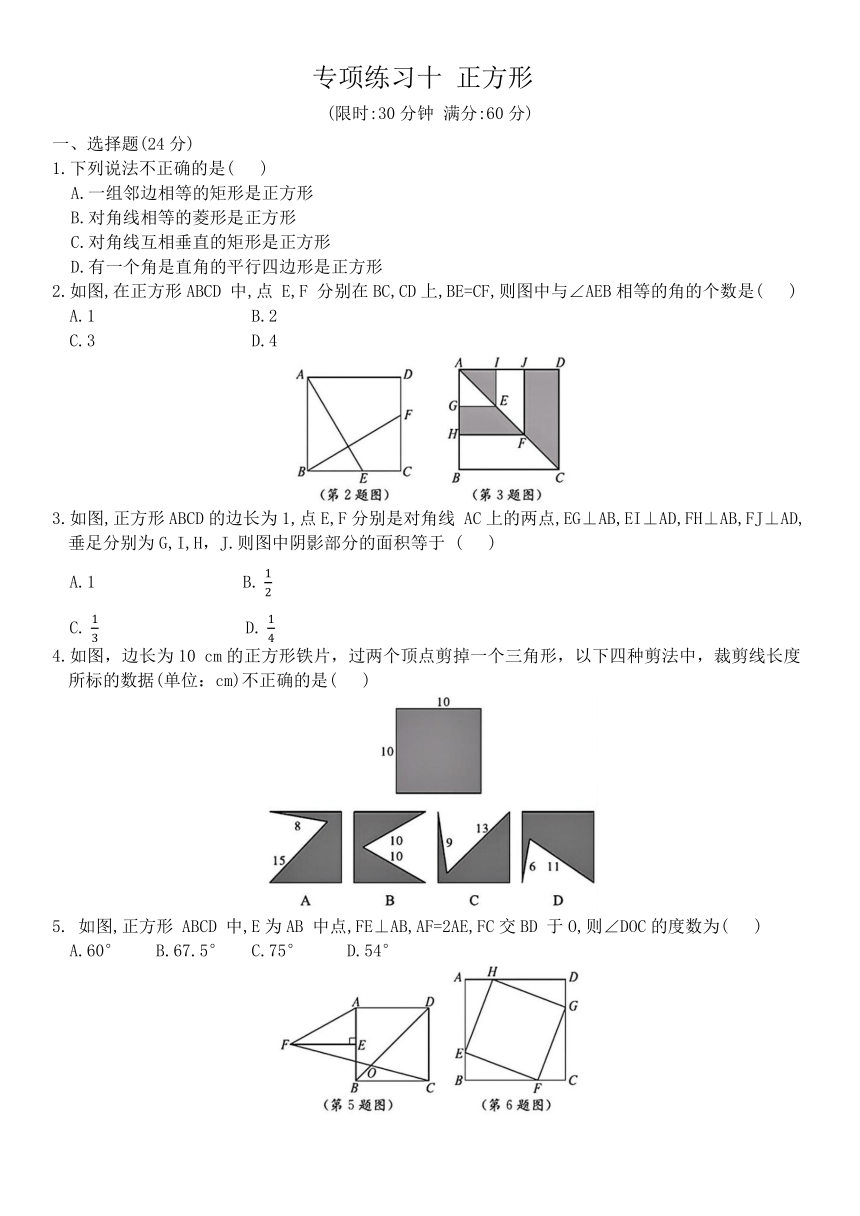
专项练习十 正方形 (限时:30分钟 满分:60分) 一、选择题(24分) 1.下列说法不正确的是( ) A.一组邻边相等的矩形是正方形 B.对角线相等的菱形是正方形 C.对角线互相垂直的矩形是正方形 D.有一个角是直角的平行四边形是正方形 2.如图,在正方形ABCD 中,点 E,F 分别在BC,CD上,BE=CF,则图中与∠AEB相等的角的个数是( ) A.1 B.2 C.3 D.4 3.如图,正方形ABCD的边长为1,点E,F分别是对角线 AC上的两点,EG⊥AB,EI⊥AD,FH⊥AB,FJ⊥AD,垂足分别为G,I,H，J.则图中阴影部分的面积等于 ( ) A.1 B. C. D. 4.如图，边长为10 cm的正方形铁片，过两个顶点剪掉一个三角形，以下四种剪法中，裁剪线长度所标的数据(单位：cm)不正确的是( ) 5. 如图,正方形 ABCD 中,E为AB 中点,FE⊥AB,AF=2AE,FC交BD 于O,则∠DOC的度数为( ) A.60° B.67.5° C.75° D.54° 6.如图，正方形ABCD的边长为8，在各边上顺次截取AE=BF=CG=DH=5,则四边形 EFGH的面积是( ) A.30 B.34 C.36 D.40 7.△ABC中,∠C=90°,点O为△ABC三条角平分线的交点,OD⊥BC 于 D,OE⊥AC于E,OF⊥AB于F,且AB=10 cm,BC=8cm ,AC=6 cm,则点O到三边AB、AC、BC的距离为( ) A. 2cm,2cm,2cm B. 3cm,3c m, 3cm C.4 cm,4 cm,4 cm D. 2cm , 3cm,5cm 8.如图,AD 是△ABC的角平分线,DE,DF分 别 是 △ABD 和△ACD的高,得到下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF 是正方形; DE .其中正确的是 ( ) A.②③ B.②④ C.②③④ D.①③④ 二、填空题(12分) 9.菱形ABCD 中,对角线 AC,BD 相交于点O，请你添加一个条件，使得菱形ABCD 成为正方形，这个条件可以是 .(写出一种情况即可) 10.如图,在正方形ABCD中,点 A(a,0),点B(0,b),a>0,b>0,则点 C 的坐标为 11.如图,E,F 是正方形ABCD 的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 . 三、解答题(24 分) 12.(12分)如图,正方形ABCD 的对角线AC与BD 交于点O,分别过点 C、点 D 作CE∥BD,DE∥AC.求证:四边形 OCED是正方形. 13.(12 分)如图,点 E 是正方形ABCD 对角线AC 上一点,EF⊥AB,EG⊥BC,垂足分别为 E,F,若正方形 ABCD 的周长是40 cm. (1)求证:四边形BFEG是矩形; (2)求四边形EFBG 的周长; (3)当AF的长为多少时,四边形 BFEG是正方形. 专项练习十 正方形 1. D 2. C 3. B 4. A 5. A 6. B 7. A 8. C 9. AC=BD(或∠ABC=90°) 10.(b,a+b) 11.8 12.证明: ∴四边形OCED是平行四边形， ∵四边形ABCD是正方形,∴OA=OC=OB=OD,AC⊥BD, ∴四边形OCED是正方形. 13.(1)证明:∵四边形ABCD为正方形, ∴AB⊥BC,∠B=90°. ∵EF⊥AB,EG⊥BC,∴EF∥GB,EG∥BF. ∵∠B=90°,∴四边形BFEG是矩形; (2)解:∵正方形ABCD的周长是40 cm, ∵四边形ABCD为正方形， 为等腰直角三角形,∴AF=EF, ∴四边形EFBG的周长 (3)解:若要四边形BFEG是正方形,只需EF=BF, ∴当AF=5cm时,四边形BFEG是正方形.