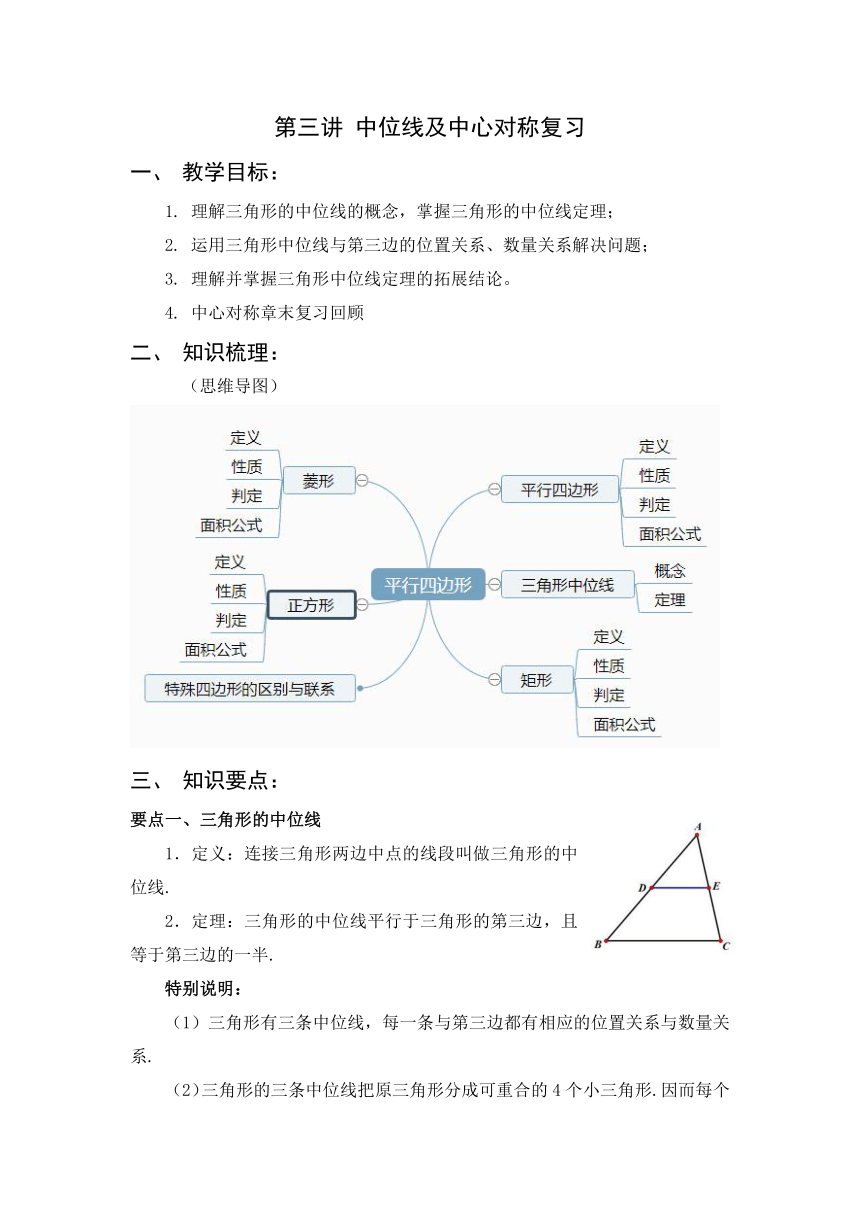
第三讲 中位线及中心对称复习 教学目标: 理解三角形的中位线的概念,掌握三角形的中位线定理; 运用三角形中位线与第三边的位置关系、数量关系解决问题; 理解并掌握三角形中位线定理的拓展结论。 中心对称章末复习回顾 知识梳理: (思维导图) 知识要点: 要点一、三角形的中位线 1.定义:连接三角形两边中点的线段叫做三角形的中位线. 2.定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半. 特别说明: (1)三角形有三条中位线,每一条与第三边都有相应的位置关系与数量关系. (2)三角形的三条中位线把原三角形分成可重合的4个小三角形.因而每个小三角形的周长为原三角形周长的,每个小三角形的面积为原三角形面积的. (3)三角形的中位线不同于三角形的中线. 要点二、中点三角形 定义:中点三角形就是把一个三角形的三边中点顺次连接起来的一个新三角形. 性质: (1)这个新三角形的各个边长分别是原来三角形三边长的一半且分别平行,角的度数与原三角形分别相等,4个三角形都全等 (2)中点三角形周长是原三角形的周长一半。 (3)中点三角形面积是原三角形面积的四分之一。 补充:中点三角形与原三角形不仅相似,而且位似。 要点三、中点四边形 定义:依次连接任意各边中点所得的四边形称为中点四边形。中点四边形的形状与原四边形的对角线的数量和位置关系有关。 性质(1)不管原四边形的形状怎样改变,中点四边形的形状始终是。 要点四、四边形的联系 例题精讲: 题型1:三角形中位线定理的认识与理解 例1():在中,,,,点,,分别为边,,的中点,则的周长为( ) A.9 B.12 C.14 D.16 变式1-1():如图,是的中线,E是的中点,F是延长线与的交点,若,则( ) A.3 B.2 C. D. 变式1-2():在RtABC中,C=90°,AC=5,BC=12,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN、MN的中点,则DE的最小值是_____. 变式1-3()(1)回顾定理:如图1,在中,是的中位线.那么与的关系有_____. (2)运用定理:如图2,在四边形中,,,点F为的中点,点E为的中点.若,,求的长. 题型2:三角形中位线定理的应用 例2():如图,的面积是,点,,,分别是,,,的中点,则的面积是_____ 变式2-1():如图,已知四边形中,,点E、F分别是边的中点,连接,则的长是( ) B.5 C. D.10 变式2-2():如图,在中,,动点在边上从点A开始向终点运动,则线段的中点从开始到停止所经过的路线长为_____cm. 变式2-3()如图,在中,,将平移5个单位长度得到,点P,Q分别是,的中点,的值不可以是( ) A.4 B.5 C.6 D.7 题型3:中点四边形的理解与应用 例3():若顺次连接四边形各边的中点所得的四边形是正方形,则四边形的两条对角线一定是( ) A.互相平分 B.互相垂直 C.互相平分且相等 D.互相垂直且相等 变式3-1():如图,四边形中,点、、、分别是线段、、、的中点,则四边形的周长( ) A.只与、的长有关 B.只与、的长有关 C.只与、的长有关 D.与四边形各边的长都有关. 变式3-2():(宋体 小四)如图,点、、、分别是四边形边、、、的中点.则下列说法: ①若,则四边形为矩形; ②若,则四边形为菱形; ③若四边形是平行四边形,则与互相平分; ④若四边形是正方形,则与互相垂直且相等. 其中正确的个数是( ) A.1 B.2 C.3 D.4 题型4:特殊四边形的性质及应用 例4():如图,在平行四边形中,的平分线与的平分线交于点E,若点E恰好在边上,则的值为_____. 变式4-1():如图,正方形ABCD的边长为3,点E在边AB上,且.若点P在对角线BD上移动,则的最小值是 _____ . 变式4-2():如图,正方形ABCD 的边长为4,E 为AB 上一点,且AE=3 ,F 为BC 边上的一个动点,连 ... ...
~~ 您好,已阅读到文档的结尾了 ~~