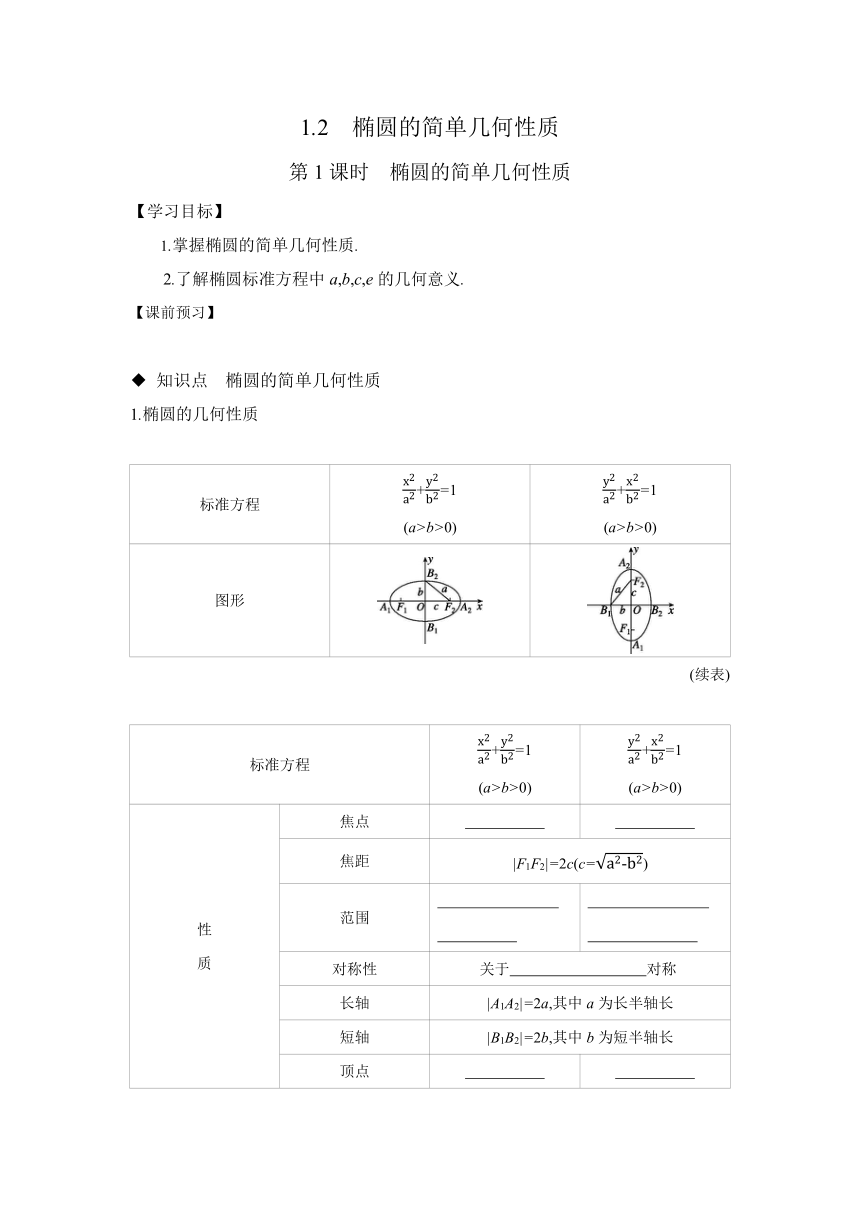
1.2 椭圆的简单几何性质 第1课时 椭圆的简单几何性质 【学习目标】 1.掌握椭圆的简单几何性质. 2.了解椭圆标准方程中a,b,c,e的几何意义. 【课前预习】 ◆ 知识点 椭圆的简单几何性质 1.椭圆的几何性质 标准方程 +=1 (a>b>0) +=1 (a>b>0) 图形 (续表) 标准方程 +=1 (a>b>0) +=1 (a>b>0) 性 质 焦点 焦距 |F1F2|=2c(c=) 范围 对称性 关于 对称 长轴 |A1A2|=2a,其中a为长半轴长 短轴 |B1B2|=2b,其中b为短半轴长 顶点 离心率 (0b>0)的长轴长是a.( ) (3)若椭圆的对称轴为坐标轴,长轴长与短轴长分别为10,8,则椭圆的方程为+=1. ( ) (4)椭圆+=1比椭圆+=1更扁一些. ( ) 【课中探究】 ◆ 探究点一 椭圆的简单几何性质 例1 求下列各椭圆的长轴长、短轴长、焦距、顶点坐标、焦点坐标和离心率: (1)+=1; (2)+=1; (3)4x2+9y2=1. 变式 [2024·兰州一中高二期中] 已知椭圆x2+=2(m>0)的离心率e=,求m的值及椭圆的长轴长、焦距、焦点坐标、顶点坐标. [素养小结] 解决椭圆几何性质问题的方法是先将所给方程化为标准形式,然后根据方程判断出椭圆的焦点在哪个坐标轴上,再利用a,b,c之间的关系和定义,求椭圆的基本量. ◆ 探究点二 椭圆的简单几何性质的应用 例2 求满足下列条件的椭圆的标准方程. (1)椭圆过点(3,0),离心率e=; (2)椭圆在x轴上的一个焦点与短轴两个端点的连线互相垂直,且其焦距为8; (3)椭圆经过点M(1,2),且与椭圆+=1有相同的离心率. 变式 已知椭圆的对称轴是坐标轴,O为坐标原点,F是一个焦点,A是一个顶点,若椭圆的长轴长是26,cos∠OFA=,则椭圆的方程是 ( ) A.+=1 B.+=1 C.+=1或+=1 D.+=1或+=1 [素养小结] 利用椭圆的几何性质求其标准方程的思路 (1)当利用椭圆的几何性质求椭圆的标准方程时,通常采用待定系数法,其步骤是: ①确定焦点的位置; ②设出相应椭圆的标准方程; ③根据已知条件列方程(组),常用的关系式有b2=a2-c2,e=等. (2)不能确定椭圆的焦点位置时,满足题意的椭圆的标准方程可能有两个. 提醒:与椭圆+=1(a>b>0)有相同离心率的椭圆的方程为+=k1(k1>0,焦点在x轴上)或+=k2(k2>0,焦点在y轴上). ◆ 探究点三 椭圆的离心率 例3 (1)若一个椭圆的长轴长2a、短轴长2b和焦距2c满足2a+2c=2×2b,则该椭圆的离心率是 ( ) A. B. C. D. (2)如图,A,B,C分别为椭圆+=1(a>b>0)的左顶点、上顶点与右焦点,若∠ABC=90°,求该椭圆的离心率. 变式 (1)[2024·黄山高二期中] 已知矩形ABCD的四个顶点都在椭圆+=1(a>b>0)上,边AD和BC分别经过椭圆的左、右焦点,且2|AB|=|BC|,则该椭圆的离心率为 ( ) A.-1+ B.2- C.-1+ D.2- (2)已知椭圆C:+=1(a>b>0),其上顶点为A,左、右焦点分别为F1,F2,且△AF1F2为等边三角形,则椭圆C的离心率为 ( ) A. B. C. D. [素养小结] 求椭圆离心率的值或范围的两种方法 (1)直接法:若已知a,c,可直接利用e=求解.若已知a,b或b,c,可借助a2=b2+c2求出c或a,再代入公式e=求解. (2)方程法:若a,c的值不可求,则可根据条件建立a,b,c的齐次关系式,借助a2=b2+c2,转化为关于a,c的齐次方程或不等式,再将方程或不等式两边同时除以a的最高次幂,得到关于e的方程或不等式,即可 ... ...
~~ 您好,已阅读到文档的结尾了 ~~