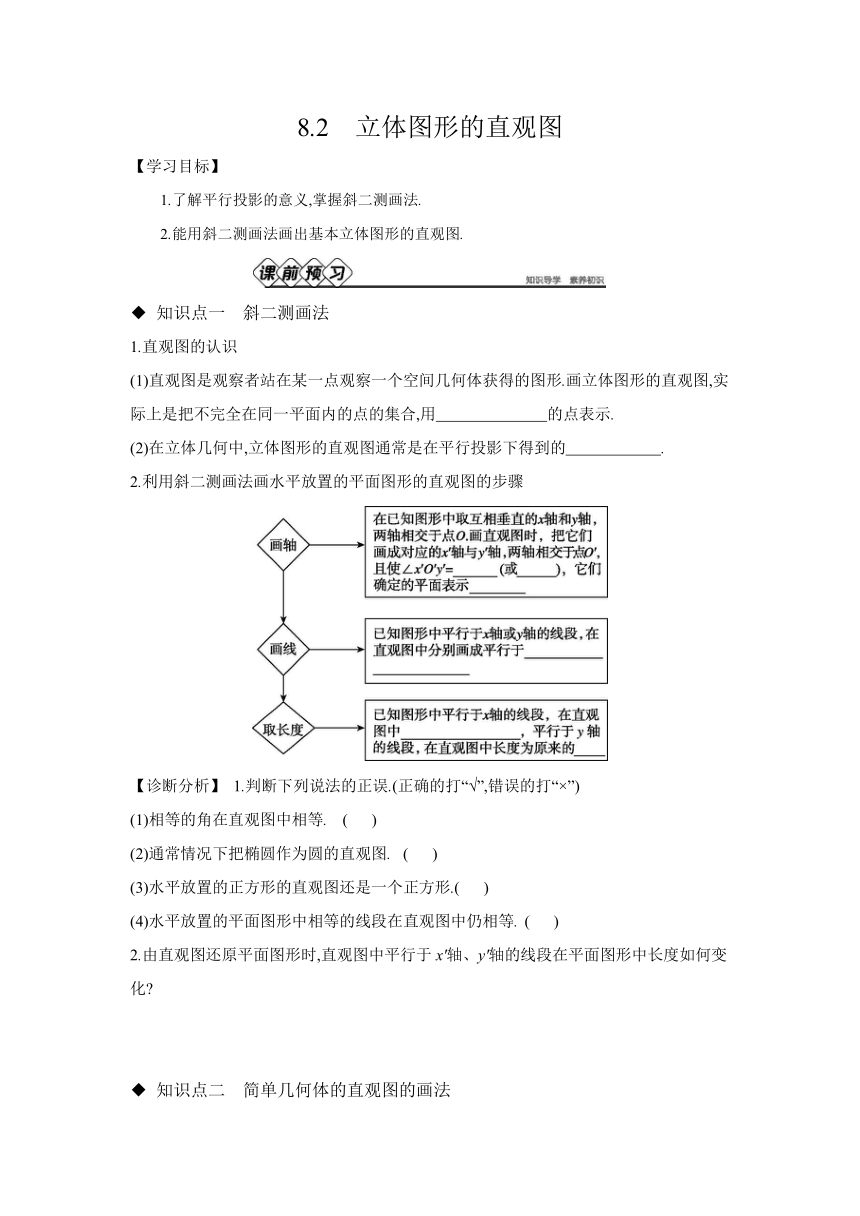
8.2 立体图形的直观图 【学习目标】 1.了解平行投影的意义,掌握斜二测画法. 2.能用斜二测画法画出基本立体图形的直观图. ◆ 知识点一 斜二测画法 1.直观图的认识 (1)直观图是观察者站在某一点观察一个空间几何体获得的图形.画立体图形的直观图,实际上是把不完全在同一平面内的点的集合,用 的点表示. (2)在立体几何中,立体图形的直观图通常是在平行投影下得到的 . 2.利用斜二测画法画水平放置的平面图形的直观图的步骤 【诊断分析】 1.判断下列说法的正误.(正确的打“√”,错误的打“×”) (1)相等的角在直观图中相等. ( ) (2)通常情况下把椭圆作为圆的直观图. ( ) (3)水平放置的正方形的直观图还是一个正方形.( ) (4)水平放置的平面图形中相等的线段在直观图中仍相等. ( ) 2.由直观图还原平面图形时,直观图中平行于x'轴、y'轴的线段在平面图形中长度如何变化 ◆ 知识点二 简单几何体的直观图的画法 画几何体的直观图时,与画平面图形的直观图相比,只是多画一个与x轴、y轴都 的z轴,并且使平行于z轴的线段的平行性和长度 . 【诊断分析】 判断下列说法的正误.(正确的打“√”,错误的打“×”) (1)图①是一个正方体的直观图. ( ) (2)若图②是一个长方体的直观图,则原长方体的高为2. ( ) ◆ 探究点一 画平面图形的直观图 例1 画出如图所示的水平放置的直角梯形(其中OB∥CD,OD⊥OB)的直观图. 变式 如图所示,在水平放置的△ABC中,BC=8 cm,BC边上的高AD=6 cm,试用斜二测画法画出其直观图. ◆ 探究点二 画空间几何体的直观图 例2 用斜二测画法画长、宽、高分别为4 cm,3 cm,2 cm的长方体的直观图. 变式 画底面半径为2 cm,高为4 cm的圆锥的直观图. [素养小结] 简单几何体直观图的画法 (1)画轴:通常以高所在直线为z轴建系. (2)画底面:根据平面图形直观图的画法确定底面. (3)确定顶点:利用与z轴平行或在z轴上的线段确定有关顶点. (4)连线成图. ◆ 探究点三 直观图的有关计算 例3 已知水平放置的△ABC按照斜二测画法画出的直观图△A'B'C'如图所示,其中B'C'=4,A'B'=2,画出△ABC的原图并求其面积. 变式 (1)如图所示的△A'B'C'是水平放置的△ABC的直观图,其中A'O'=B'O'=C'O'=1,则原△ABC是一个 ( ) A.等边三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形 (2)用斜二测画法画一个水平放置的平面图形ABCD的直观图,得到四边形A'B'C'D',如图所示,已知A'B'=3,B'C'=1,A'D'=3,且A'D'∥B'C'. ①求原平面图形ABCD的面积; ②将原平面图形ABCD绕BC旋转一周,判断所形成的几何体的形状. [素养小结] 由直观图还原为平面图形的关键是找与x'轴、y'轴平行的直线或线段,且平行于x'轴的线段还原时长度不变,平行于y'轴的线段还原时放大为直观图中相应线段长的2倍,由此确定图形的各个顶点,顺次连接即可.由此可得,直观图面积S'与原图形面积S的关系为S'=S或S=2S'. 8.2 立体图形的直观图 【课前预习】 知识点一 1.(1)同一平面内 (2)平面图形 2.45° 135° 水平面 x'轴或y'轴的线段 保持原长度不变 一半 诊断分析 1.(1)× (2)√ (3)× (4)× [解析] (1)如正方形(四个内角都相等)的直观图为平行四边形(相邻的内角互补,相对的内角相等). (2)生活经验告诉我们,水平放置的圆看起来像椭圆,因此我们一般用椭圆作为圆的直观图. (3)水平放置的正方形的直观图是一个平行四边形. (4)水平放置的正方形的直观图中邻边不相等. 2.解:在直观图中平行于x'轴的线段在平面图形中长度不变,但平行于y'轴的线段在平面图形中长度变为原来的2倍. 知识点二 垂直 都不变 诊断分析 (1)× (2)× [解析] (1)被遮挡住的三条棱应画为虚线,如图所示. (2)原长方体中的高线与z轴平行,而与z轴 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

