2025人教A版高中数学必修第二册强化练习题--专题强化练10　平面图形的翻折问题

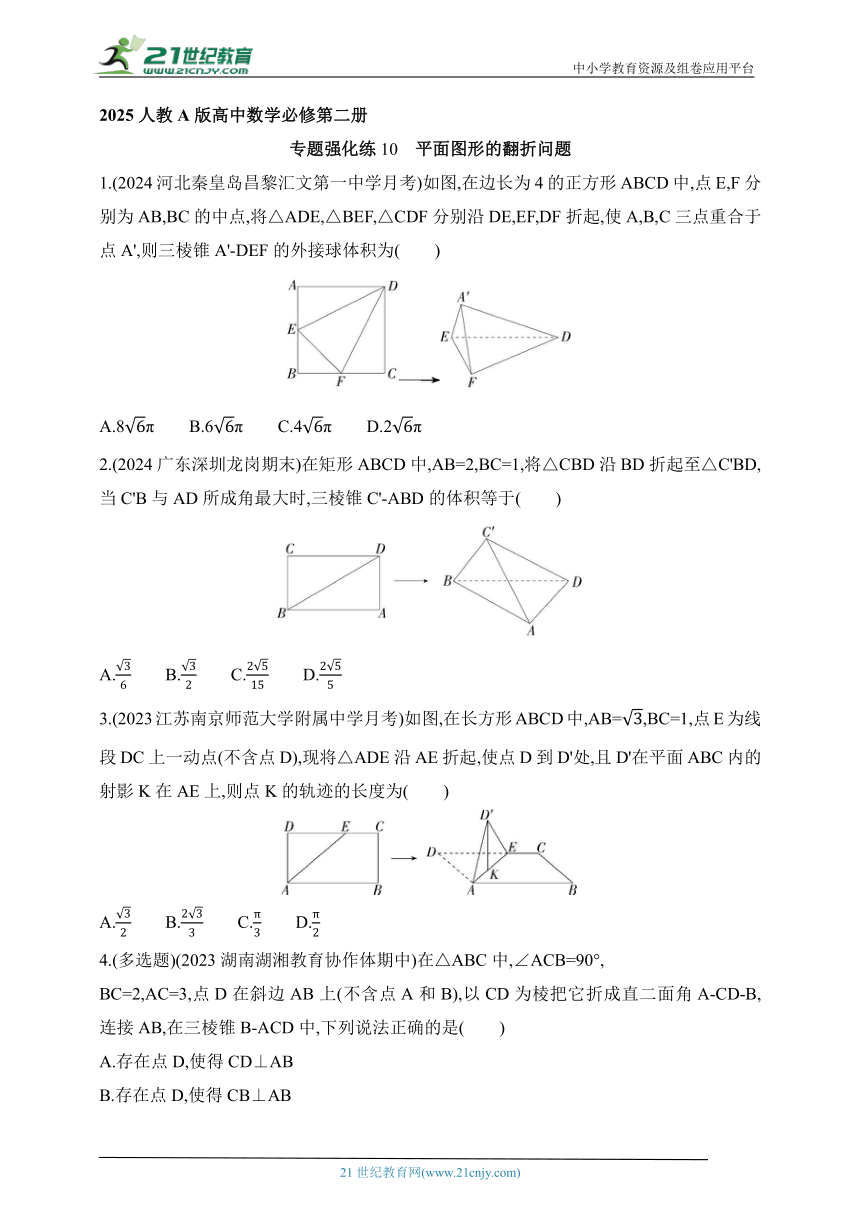
中小学教育资源及组卷应用平台 2025人教A版高中数学必修第二册 专题强化练10　平面图形的翻折问题 1.(2024河北秦皇岛昌黎汇文第一中学月考)如图,在边长为4的正方形ABCD中,点E,F分别为AB,BC的中点,将△ADE,△BEF,△CDF分别沿DE,EF,DF折起,使A,B,C三点重合于点A',则三棱锥A'-DEF的外接球体积为(　　) A.8π　　B.6π　　C.4π　　D.2π 2.(2024广东深圳龙岗期末)在矩形ABCD中,AB=2,BC=1,将△CBD沿BD折起至△C'BD,当C'B与AD所成角最大时,三棱锥C'-ABD的体积等于(　　) A.　　B.　　C.　　D. 3.(2023江苏南京师范大学附属中学月考)如图,在长方形ABCD中,AB=,BC=1,点E为线段DC上一动点(不含点D),现将△ADE沿AE折起,使点D到D'处,且D'在平面ABC内的射影K在AE上,则点K的轨迹的长度为(　　) A.　　B.　　C.　　D. 4.(多选题)(2023湖南湖湘教育协作体期中)在△ABC中,∠ACB=90°, BC=2,AC=3,点D在斜边AB上(不含点A和B),以CD为棱把它折成直二面角A-CD-B,连接AB,在三棱锥B-ACD中,下列说法正确的是(　　) A.存在点D,使得CD⊥AB B.存在点D,使得CB⊥AB C.若在原三角形ABC中,CD⊥AB,则折成的三棱锥B-ACD的外接球的表面积为 D.AB的最小值为 5.(多选题)(2024四川成都列五中学月考)如图,将一副三角尺拼成平面四边形,将等腰直角△ABC沿BC向上翻折,得三棱锥A-BCD,设CD=2,点E,F分别为棱BC,BD的中点,M为线段AE上的动点,下列说法正确的是(　　) A.在翻折过程中,不存在某个位置使得AC⊥CD B.若AB⊥CD,则AD与平面BCD所成角的正切值为 C.当三棱锥A-BCD的体积取得最大值时,AD与平面ABC所成角的正弦值为 D.当AB=AD时,CM+FM的最小值为 6.(2024吉林梅河口第五中学期末)在矩形ABCD中,AB=1,BC=2,将△ABD沿BD向上折起到△A1BD的位置,得到四面体A1-BCD.当四面体A1-BCD的体积最大时,异面直线A1B与CD所成角的余弦值为　　　　. 7.(2024上海大学附属中学月考)如图所示,在矩形ABCD中,AB=2,AD=2,沿BD将△BCD折起,使得点C在平面ABD上的射影落在AB上,则直线BC与平面ABD所成的角为　　　　. 8.(2024四川成都第七中学期末)如图1,在梯形BCDE中,BC∥DE,BA⊥DE,且EA=DA=AB=2CB=2,如图2,沿AB将四边形ABCD折起,使得平面ABCD与平面ABE垂直,M为CE的中点. (1)求证:BC∥平面DAE; (2)求证:AM⊥BE; (3)求点D到平面BCE的距离. 　　 9.(2022江西宜春奉新第一中学月考)如图,在梯形ABCD中,AB∥DC, AB=2AD=2DC=4,E,F分别是AD,BC的中点,且EF交AC于点O,现将梯形ABCD沿对角线AC翻折成直二面角D1-A1C1-B1. (1)证明:A1B1∥平面O1E1F1; (2)证明:C1B1⊥D1A1; (3)若∠ADC=60°,在线段D1B1上是否存在点M,使得三棱锥D1-A1C1M的体积为 若存在,求出的值;若不存在,请说明理由. 答案与分层梯度式解析 专题强化练10　平面图形的翻折问题 1.A 2.A 3.C 4.ACD 5.BC 1.A　依题意得A'D⊥A'E,A'E⊥A'F,A'D⊥A'F,且A'D=4,A'E=A'F=2, 于是三棱锥A'-DEF可以补形成以A'D,A'E,A'F为相邻三条棱的长方体,该长方体与三棱锥A'-DEF的外接球相同, 设三棱锥A'-DEF的外接球的半径为R,则2R为长方体的体对角线长,即2R==2,所以R=, 所以三棱锥A'-DEF的外接球体积为π×()3=8π.故选A. 2.A　因为异面直线所成角的范围是,故当C'B⊥AD时,C'B与AD所成角最大, 因为四边形ABCD是矩形,所以AB⊥AD, 因为AB∩C'B=B,AB,C'B 平面ABC', 所以AD⊥平面ABC', 因为AC' 平面ABC',所以AD⊥AC', 在直角三角形ADC'中,AC'==, 所以BC'2+AC'2=AB2,所以BC'⊥AC', 所以VC'-ABD=VD-ABC'=S△ABC'·AD=××1××1=.故选A. 3.C　由题意知D'K⊥平面ABC,又D'K 平面AED',所以平面AED'⊥平面ABC,如图1,连接DK,则DK⊥AE,故点K在以AD为直径的圆上, 取AD的中点O,连接KO,则KO=. 　 如图2,当E与C重合时,△AKD∽△CBA,所以=,则AK=. 设M在AC上,且AM=,则点K的轨迹是以AD为直径的 ... ...