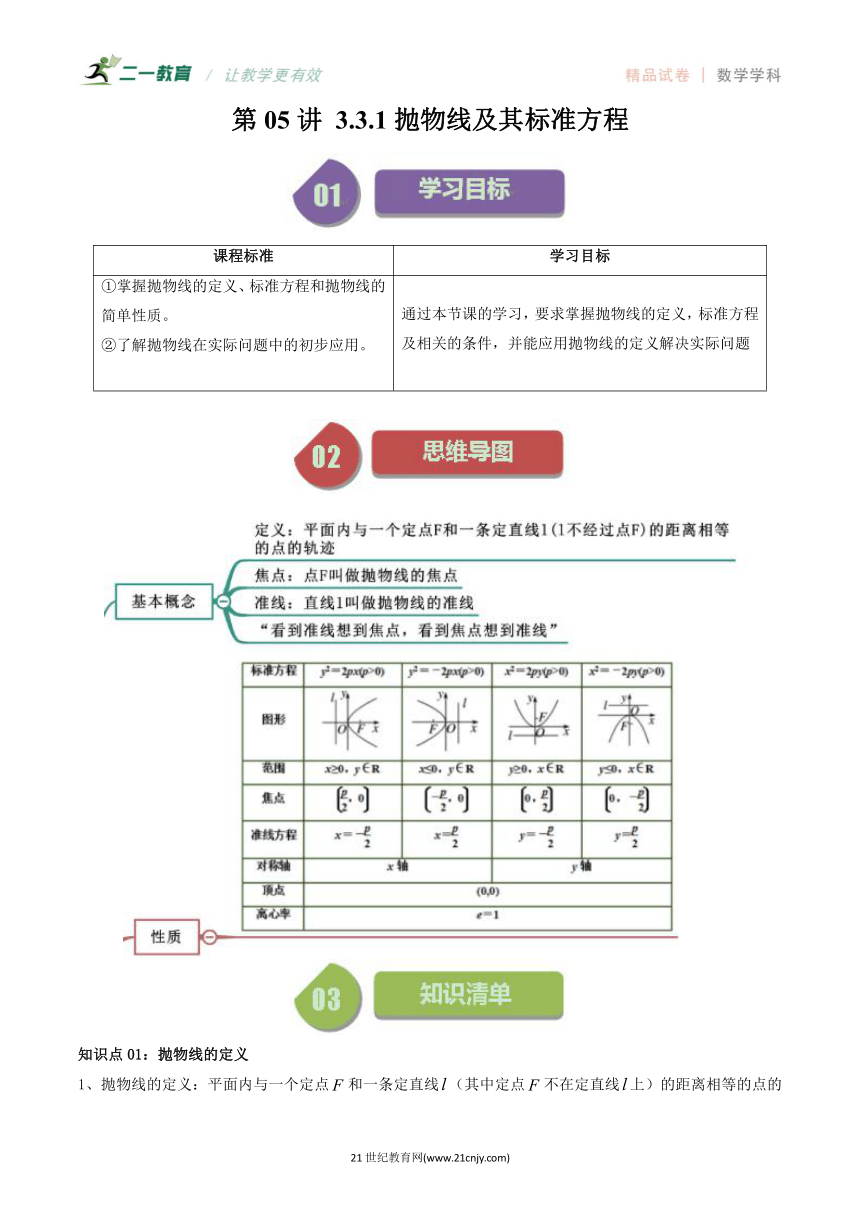
第05讲 3.3.1抛物线及其标准方程 课程标准 学习目标 ①掌握抛物线的定义、标准方程和抛物线的简单性质。 ②了解抛物线在实际问题中的初步应用。 通过本节课的学习,要求掌握抛物线的定义,标准方程及相关的条件,并能应用抛物线的定义解决实际问题 知识点01:抛物线的定义 1、抛物线的定义:平面内与一个定点和一条定直线(其中定点不在定直线上)的距离相等的点的轨迹叫做抛物线,定点叫做抛物线的焦点,定直线叫做抛物线的准线. 2、抛物线的数学表达式:(为点到准线的距离). 【即学即练1】(2023春·四川凉山·高二宁南中学校联考期末)已知抛物线上一点P到y轴的距离为2,焦点为F,则( ) A.2 B.3 C. D. 【答案】B 【详解】由题得抛物线的准线方程为, 所以点P到准线的距离为, 由抛物线的定义得3. 故选:B 知识点02:抛物线的标准方程 设,抛物线的标准方程、类型及其几何性质: 方程 () () () () 图形 焦点 准线 【即学即练2】(2023秋·高二课时练习)已知抛物线的标准方程如下,分别求其焦点和准线方程: (1); (2). 【答案】(1)焦点为,准线方程为; (2)焦点为,准线方程为. 【详解】(1)由抛物线方程为,可得,且焦点在轴正半轴上, 所以可得其焦点为,准线方程为; (2)将化成标准方程为, 可得,且焦点在轴负半轴上, 所以焦点为,准线方程为. 特别说明: 1、要注意弄清抛物线四种形式的标准方程的特征及其对应抛物线的形状(焦点位置、开口方向等).抛物线的标准方程中,有一个一次项和一个二次项,二次项的系数为1,一次项的系数为;若一次项的字母是,则焦点就在轴上,若其系数是正的,则焦点就在轴的正半轴上(开口向右),若系数是负的,焦点就在轴的负半轴上(开口向左);若一次项的字母是,则焦点就在轴上,若其系数是正的,则焦点就在轴的正半轴上(开口向上),若系数是负的,焦点就在轴的负半轴上(开口向下). 2、焦点的非零坐标是标准方程下一次项系数的 . 3、准线与坐标轴的交点和抛物线的焦点关于原点对称. 4、(1)通径:过焦点且垂直于对称轴的弦长等于,通径是过焦点最短的弦. (2)抛物线()上一点到焦点的距离,也称为抛物线的焦半径. 题型01抛物线定义的理解 【典例1】(2023秋·陕西西安·高二统考期末)若抛物线上一点到轴的距离为,则点到抛物线的焦点的距离为 . 【典例2】(2023·四川成都·四川省成都列五中学校考三模)若抛物线上的点P到焦点的距离为8,到轴的距离为6,则抛物线的标准方程是( ) A. B. C. D. 【变式1】(2023春·陕西榆林·高二统考期末)已知抛物线的焦点为,点在上,若到直线的距离为7,则 . 【变式2】(2023春·江西宜春·高三江西省宜春中学校考阶段练习)若抛物线上一点到焦点的距离是该点到轴距离的3倍,则 . 题型02利用抛物线定义求方程 【典例1】(2023春·江西·高三校联考阶段练习)设圆与y轴交于A,B两点(A在B的上方),过B作圆O的切线l,若动点P到A的距离等于P到l的距离,则动点P的轨迹方程为( ) A. B. C. D. 【典例2】(2023·全国·高三专题练习)已知动点的坐标满足,则动点的轨迹方程为 . 【变式1】(2023·全国·高三专题练习)已知点,过点且与y轴垂直的直线为,轴,交于点N,直线l垂直平分FN,交于点M. 求点M的轨迹方程; 【变式2】(2023·全国·高三专题练习)动点到y轴的距离比它到定点的距离小2,求动点的轨迹方程. 题型03抛物线上点到定点距离及最值 【典例1】(2023春·河南焦作·高二统考开学考试)已知点A是抛物线上的点,点,则的最小值为( ) A. B.2 C. D. 【典例2】(2023春·云南昭通·高三校考阶段练习)抛物线上任意一点P到点的距离最小值为 . 【变式1】(2023·全国·高三专题练习)动点在抛物线上,则点到点的距离的 ... ...
~~ 您好,已阅读到文档的结尾了 ~~