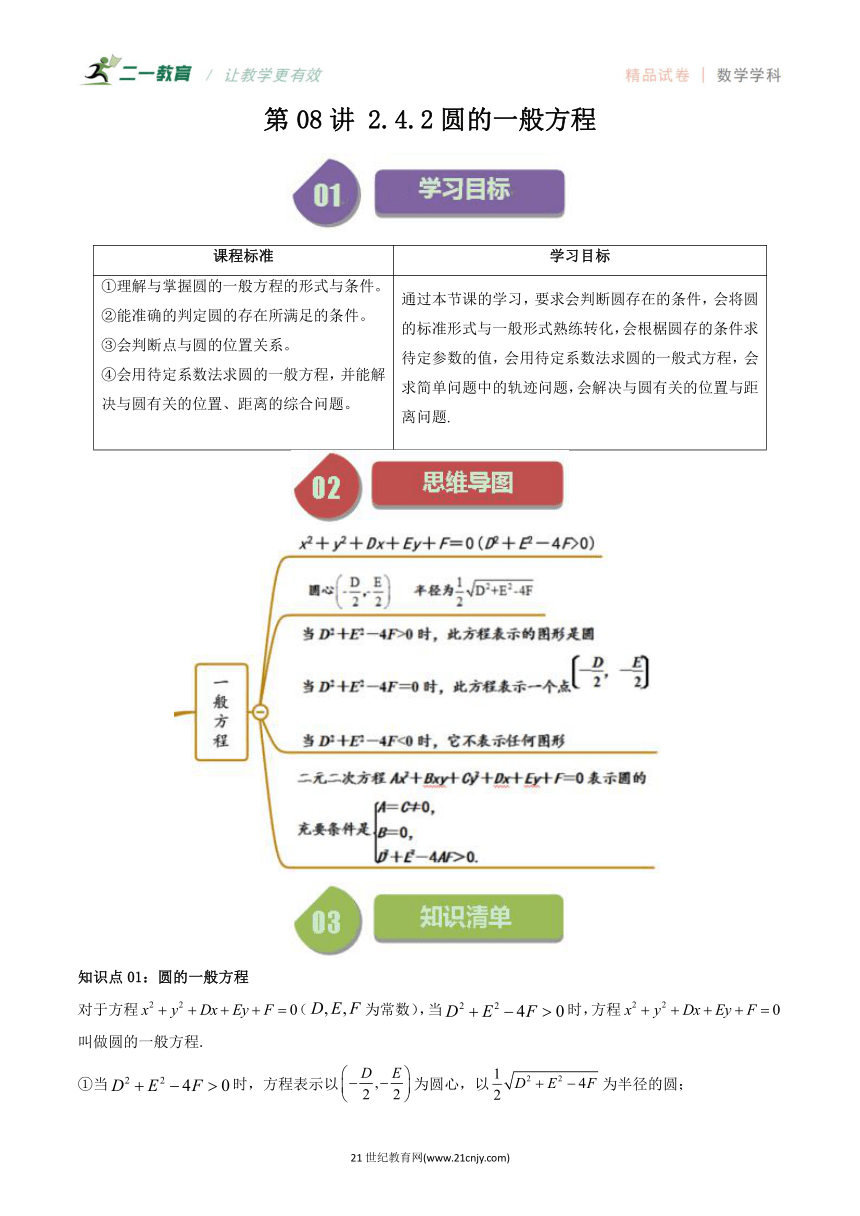
第08讲 2.4.2圆的一般方程 课程标准 学习目标 ①理解与掌握圆的一般方程的形式与条件。 ②能准确的判定圆的存在所满足的条件。 ③会判断点与圆的位置关系。 ④会用待定系数法求圆的一般方程,并能解决与圆有关的位置、距离的综合问题。 通过本节课的学习,要求会判断圆存在的条件,会将圆的标准形式与一般形式熟练转化,会根椐圆存的条件求待定参数的值,会用待定系数法求圆的一般式方程,会求简单问题中的轨迹问题,会解决与圆有关的位置与距离问题. 知识点01:圆的一般方程 对于方程(为常数),当时,方程叫做圆的一般方程. ①当时,方程表示以为圆心,以为半径的圆; ②当时,方程表示一个点 ③当时,方程不表示任何图形 说明:圆的一般式方程特点:①和前系数相等(注意相等,不一定要是1)且不为0;②没有项;③. 【即学即练1】(多选)(2022秋·高二课时练习)(多选题)下列方程不是圆的一般方程的有( ) A. B. C. D. 【答案】BCD 【详解】根据二元二次方程表示圆的条件, 对于A中,方程,可得, 所以方程是圆的一般方程; 对于B中,方程,可得, 所以方程不是圆的一般方程; 对于C中,方程中,和的系数不相等, 所以方程不是圆的一般方程; 对于D中,方程中,存在项,所以方程不是圆的一般方程. 故选:BCD. 知识点02:圆的一般方程与圆的标准方程的特点 圆的标准方程 圆的一般方程 方程 () 圆心 半径 知识点03:在圆的一般方程中,判断点与圆的位置关系 已知点和圆的一般式方程:(), 则点与圆的位置关系: ①点在外 ②点在上 ③点在内 【即学即练2】(2022·高二课时练习)点与圆的位置关系是_____.(填“在圆内”、“在圆上”、“在圆外”) 【答案】在圆内 【详解】圆的圆心坐标为,半径为2 点到圆心的距离, 因为,所以点在圆内. 故答案为:在圆内 题型01圆的一般方程的理解 【典例1】(2022秋·安徽合肥·高二合肥市第七中学校联考期中)已知方程表示圆,则的取值范围是( ) A. B. C. D. 【典例2】(2023·高二课时练习)方程表示圆的充要条件是_____. 【变式1】(2022秋·河南许昌·高二禹州市高级中学校考阶段练习)方程表示圆,则实数的可能取值为( ) A. B.2 C.0 D. 【变式2】(2023春·上海宝山·高二统考期末)若表示圆,则实数的值为_____. 题型02求圆的一般方程 【典例1】(2023·高二课时练习)过三点的圆的一般方程为( ) A. B. C. D. 【典例2】(2023·新疆克拉玛依·高二克拉玛依市高级中学校考期中)求适合下列条件的圆的方程: (1)圆心在直线上,且过点的圆; (2)过三点的圆. 【典例3】(2023·高二课时练习)已知圆经过两点,,且圆心在直线上,则圆的一般方程为_____;若直线的方程(),圆心到直线的距离是1,则的值是_____. 【变式1】(2023·江苏·高二假期作业)过坐标原点,且在轴和轴上的截距分别为2和3的圆的方程为( ) A. B. C. D. 【变式2】(2023·江苏苏州·高二苏州中学校考期中)在平面直角坐标系中,已知的顶点,边上中线所在直线方程为,边上的高所在直线方程为,求: (1)顶点的坐标; (2)外接圆的一般方程. 题型03圆的一般方程与标准方程转化 【典例1】(2023·高二课时练习)若圆的圆心到直线的距离为,则实数的值为( ) A.0或2 B.0或-2 C.0或 D.-2或2 【典例2】(2023秋·内蒙古巴彦淖尔·高二校考期末)若点为圆的弦的中点,则弦所在直线的方程为( ) A. B. C. D. 【典例3】(2023秋·高二课时练习)求圆关于直线的对称圆方程. 【变式1】(2023春·山东青岛·高二校联考期中)圆上的点到直线的最大距离是( ) A. B. C. D. 【变式2】(2023春·辽宁朝阳·高二校联考期中)已知点在圆 上,则点到轴的距离的最大值为( ) A ... ...
~~ 您好,已阅读到文档的结尾了 ~~