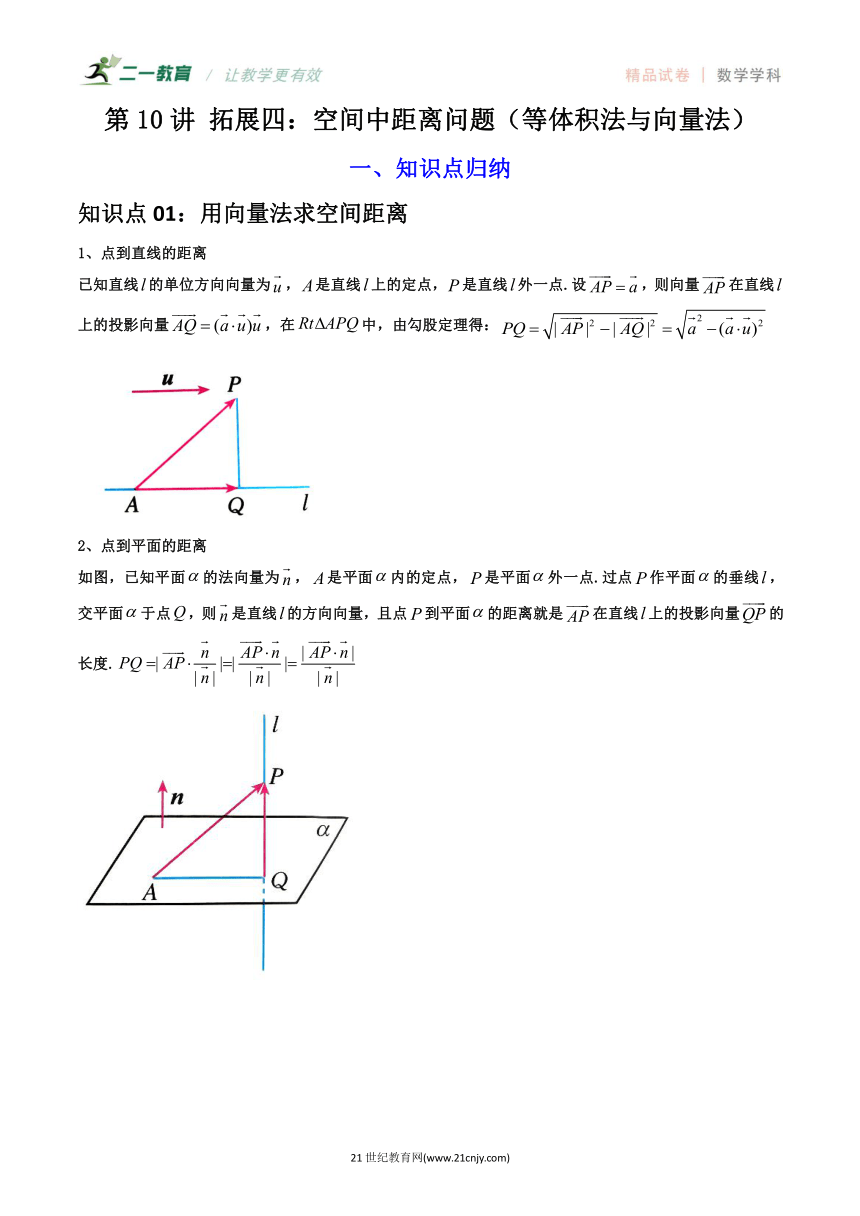
第10讲 拓展四:空间中距离问题(等体积法与向量法) 一、知识点归纳 知识点01:用向量法求空间距离 1、点到直线的距离 已知直线的单位方向向量为,是直线上的定点,是直线外一点.设,则向量在直线上的投影向量,在中,由勾股定理得: 2、点到平面的距离 如图,已知平面的法向量为,是平面内的定点,是平面外一点.过点作平面的垂线,交平面于点,则是直线的方向向量,且点到平面的距离就是在直线上的投影向量的长度. 二、题型精讲 题型01利用向量法求点到直线的距离 【典例1】(2023春·四川雅安·高二雅安中学校考期中)直线的方向向量为,且l过点,则点到直线的距离为( ) A. B. C. D. 【典例2】(2023秋·吉林长春·高二长春吉大附中实验学校校考期末)已知,,,则点到直线的距离为( ) A. B. C. D. 【典例3】(2023春·江苏淮安·高二淮阴中学校联考阶段练习)已知点,若点和点在直线上,则点到直线的距离为_____. 【变式1】(2023秋·天津·高二校联考期末)已知空间内三点,,,则点到直线的距离是( ). A. B.1 C. D. 【变式2】(2023春·福建福州·高二校联考期中)已知空间中三点,则点到直线的距离为_____. 题型02点到平面的距离等体积法 【典例1】(2023春·天津河西·高一天津市第四十二中学校考阶段练习)如图,直三棱柱的体积为6,的面积为,则点到平面的距离为( ) A. B. C.2 D. 【典例2】(2023春·四川德阳·高二德阳五中校考阶段练习)如图,在四棱锥中,已知底面是正方形,底面,且是棱上一点. (1)若平面,证明:是的中点. (2)线段上存在点,使得,求到平面的距离. 【典例3】(2023春·安徽·高一安徽省郎溪中学校联考阶段练习)已知空间几何体中,是边长为2的等边三角形,是腰长为2的等腰三角形,,,,. (1)作出平面与平面的交线,并说明理由; (2)求点到平面的距离. 【典例4】(2023春·陕西商洛·高二镇安中学校考期中)如图,在四棱锥中,已知棱两两垂直且长度分别为1,1,2,,. (1)若中点为,证明:平面; (2)求点到平面的距离. 【变式1】(2023春·重庆·高一重庆一中校考期中)如图所示,在四棱锥中,四边形为等腰梯形,. (1)证明:平面: (2)若,求点到平面的距离. 【变式2】(2023·上海·高三专题练习)如图,在正三棱柱中,已知,是的中点. (1)求直线与所成的角正切值 (2)求证:平面平面,并求点到平面的距离. 【变式3】(2023·河南·许昌实验中学校联考二模)在四棱锥中,四边形为等腰梯形,,,,. (1)证明:平面平面. (2)若,,求点到平面的距离. 【变式4】(2023·全国·高一专题练习)如图所示,在长方体中,,,且E为中点.求到平面的距离. 题型03点到平面的距离的向量法 【典例1】(2023春·浙江温州·高二校联考期末)如图所示,在棱长为1的正方体中为线段的中点. (1)求证:平面平面; (2)求到平面的距离. 【典例2】(2023春·高二单元测试)如图,四棱锥中,底面为矩形,侧面为正三角形,,,平面平面,为棱上一点(不与重合),平面交棱于点. (1)求证:; (2)若二面角的余弦值为,求点到平面的距离. 【典例3】(2023秋·山西晋中·高二统考期末)在正方体中,为的中点,过的平面截此正方体,得如图所示的多面体,为直线上的动点. (1)点在棱上,当时,平面,试确定动点在直线上的位置,并说明理由; (2)若为底面的中心,求点到平面的最大距离. 【变式1】(2023春·江西宜春·高二江西省清江中学校考期中)在棱长为4的正方体中,点P在棱上,且. (1)求直线与平面所成的角的正弦值大小; (2)求点到平面的距离. 【变式2】(2023春·重庆·高三重庆一中校考阶段练习)如图所示的几何体是一个半圆柱,点是半圆弧上一动点(点与点,不重合),为弧的中点,. (1) ... ...
~~ 您好,已阅读到文档的结尾了 ~~