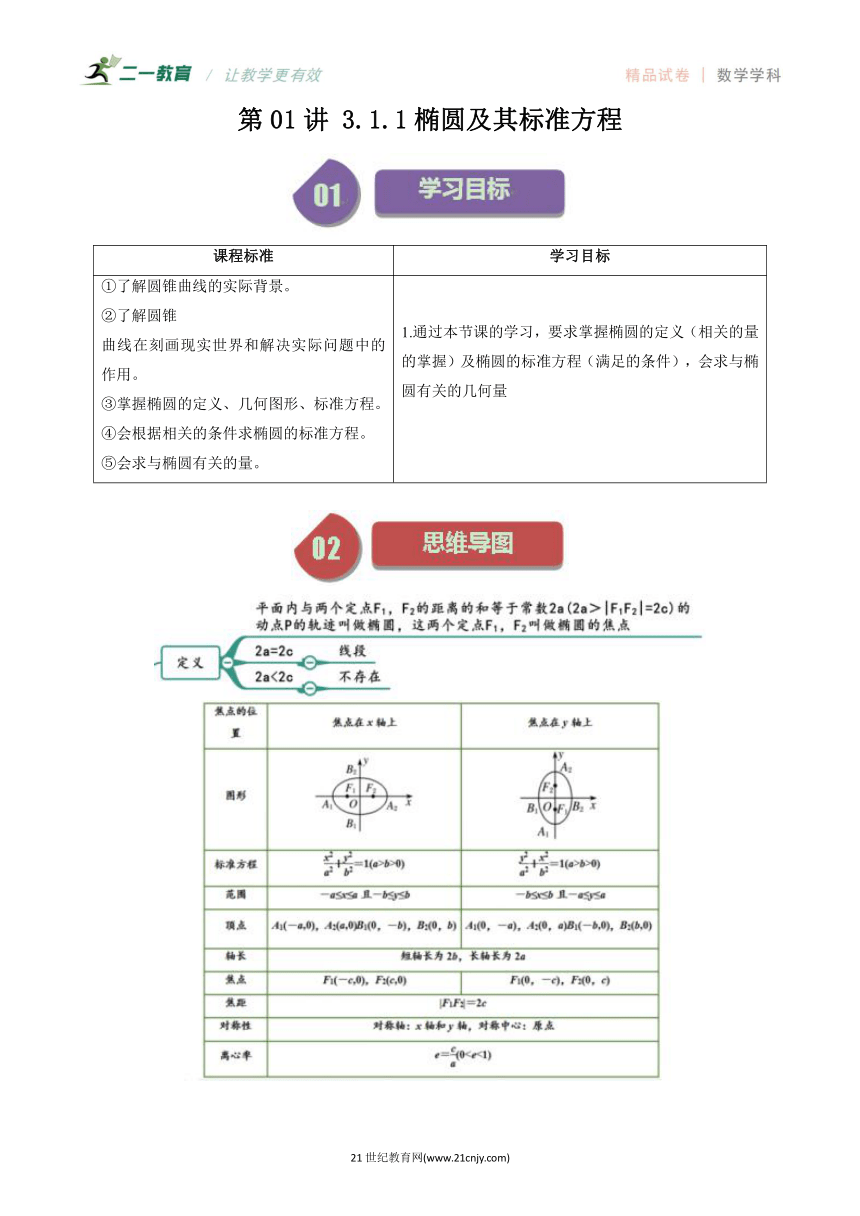
第01讲 3.1.1椭圆及其标准方程 课程标准 学习目标 ①了解圆锥曲线的实际背景。 ②了解圆锥 曲线在刻画现实世界和解决实际问题中的作用。 ③掌握椭圆的定义、几何图形、标准方程。 ④会根据相关的条件求椭圆的标准方程。 ⑤会求与椭圆有关的量。 1.通过本节课的学习,要求掌握椭圆的定义(相关的量的掌握)及椭圆的标准方程(满足的条件),会求与椭圆有关的几何量 知识点01:椭圆的定义 1、椭圆的定义:平面内一个动点到两个定点、的距离之和等于常数, 这个动点的轨迹叫椭圆. 这两个定点(,)叫椭圆的焦点,两焦点的距离()叫作椭圆的焦距. 说明: 若,的轨迹为线段; 若,的轨迹无图形 2、定义的集合语言表述 集合. 【即学即练1】(2023秋·四川南充·高二四川省南充高级中学校考期末)设定点,,动点P满足条件,则点P的轨迹是( ) A.椭圆 B.线段 C.不存在 D.椭圆或线段 【答案】A 【详解】因为,,所以, 所以,所以点P的轨迹是以,为焦点的椭圆. 故选:A. 知识点02:椭圆的标准方程 焦点位置 焦点在轴上 焦点在轴上 标准方程 () () 图象 焦点坐标 , , 的关系 【即学即练2】(2023秋·广东广州·高二广州市第八十六中学校考期末)已知的周长为20,且顶点,则顶点的轨迹方程是( ) A. B. C. D. 【答案】B 【详解】错解: ∵△ABC的周长为20,顶点, ∴|BC|=8,|AB|+|AC|=20-8=12, ∵12>8, ∴点A到两个定点的距离之和等于定值, ∴点A的轨迹是椭圆, ∵a=6,c=4, ∴b2=20, ∴椭圆的方程是 故选:D. 错因: 忽略了A、B、C三点不共线这一隐含条件. 正解: ∵△ABC的周长为20,顶点, ∴|BC|=8,|AB|+|AC|=20-8=12, ∵12>8, ∴点A到两个定点的距离之和等于定值, ∴点A的轨迹是椭圆, ∵a=6,c=4, ∴b2=20, ∴椭圆的方程是 故选:B. 特别说明: 1、两种椭圆,()的相同点是:它们的形状、大小都相同,都有,;不同点是:两种椭圆的位置不同,它们的焦点坐标也不同. 2、给出椭圆方程(,,),判断该方程所表示的椭圆的焦点位置的方法是:椭圆的焦点在轴上 标准方程中项的分母较大;椭圆的焦点在轴上 标准方程中项的分母较大,这是判断椭圆焦点所在坐标轴的重要方法.可简记作:焦点位置看大小,焦点跟着大的跑. 题型01椭圆的定义及辨析 【典例1】(2023春·新疆塔城·高二统考开学考试)设满足:,则点的轨迹为( ) A.圆 B.椭圆 C.线段 D.不存在 【典例2】.(2023·全国·高三专题练习)已知,是两个定点,且(是正常数),动点满足,则动点的轨迹是( ) A.椭圆 B.线段 C.椭圆或线段 D.直线 【变式1】(2023·全国·高二专题练习)如果点在运动过程中,总满足关系式,则点的轨迹是( ). A.不存在 B.椭圆 C.线段 D.双曲线 【变式2】(2023秋·四川成都·高二统考期末)椭圆上一点P与它的一个焦点的距离等于6,那么点P与另一个焦点的距离等于 . 题型02利用椭圆定义求方程 【典例1】(2023·上海·高二专题练习)方程,化简的结果是( ) A. B. C. D. 【典例2】(2023秋·广东广州·高二西关外国语学校校考期末)已知圆,圆,动圆M与圆外切,同时与圆内切,则动圆圆心M的轨迹方程为( ) A. B. C. D. 【变式1】(2023春·江苏南京·高二江苏省江浦高级中学校联考阶段练习)已知椭圆的左、右焦点为,且过点则椭圆标准方程为 . 【变式2】(2023·高二课时练习)已知动点M到定点与的距离的和是,则点M的轨迹方程是 . 题型03椭圆上点到焦点距离(含最值)问题 【典例1】(2023·全国·高三专题练习)已知椭圆上一点到右准线的距离为,则点到它的左焦点的距离为( ) A. B. C. D. 【典例2】(2023秋·陕西宝鸡·高二统考期末)已知椭圆上的动点到右焦点距离的最大值为, ... ...
~~ 您好,已阅读到文档的结尾了 ~~