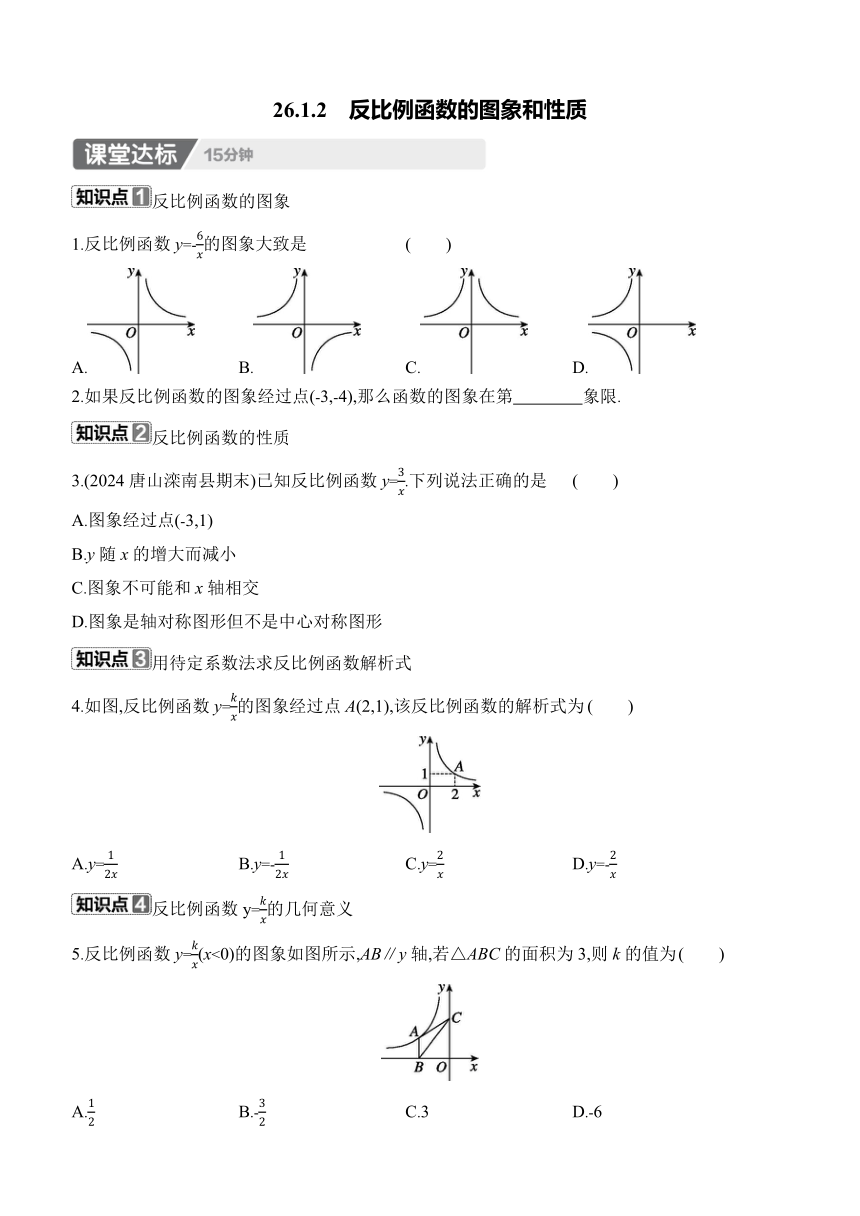
26.1.2　反比例函数的图象和性质 课时作业（含答案） 2024-2025学年数学人教版九年级下册

26.1.2　反比例函数的图象和性质 反比例函数的图象 1.反比例函数y=-的图象大致是 (　　) A. B. C. D. 2.如果反比例函数的图象经过点(-3,-4),那么函数的图象在第　　　　象限. 反比例函数的性质 3.(2024唐山滦南县期末)已知反比例函数y=.下列说法正确的是 (　　) A.图象经过点(-3,1) B.y随x的增大而减小 C.图象不可能和x轴相交 D.图象是轴对称图形但不是中心对称图形 用待定系数法求反比例函数解析式 4.如图,反比例函数y=的图象经过点A(2,1),该反比例函数的解析式为 (　　) A.y= B.y=- C.y= D.y=- 反比例函数y=的几何意义 5.反比例函数y=(x<0)的图象如图所示,AB∥y轴,若△ABC的面积为3,则k的值为 (　　) A. B.- C.3 D.-6 6.如图,矩形OABC的面积是4,点B在反比例函数y=的图象上.此反比例函数的解析式为　　　　. 7.(2024龙岩期末)如图,反比例函数y=的图象的一支位于第一象限. (1)该函数图象的另一支在第　　　　象限,k的取值范围是　　　　　. (2)点A在反比例函数的图象上,点A关于x轴的对称点为点B,点A关于原点的对称点为点C.若△ABC的面积为4,求k的值. 1.如图,满足函数y=k(x-1)和y=(k≠0)的大致图象是 (　　) ① ② ③ ④ A.①② B.②③ C.②④ D.①④ 2.对于反比例函数y=-,下列说法正确的是 (　　) A.图象经过点(2,-3) B.图象位于第一、第三象限 C.y随x的增大而增大 D.当00)的图象于点Q,S△OQC=,则k的值是　　　　;点Q的坐标为　　　　. 4.如图,在平面直角坐标系中,△AOB的边OB在y轴上,边AB与x轴交于点D,且BD=AD,反比例函数y=(x>0)的图象经过点A.若S△OAB=1,则反比例函数的解析式为　　　　. 5.如图,在△ABC中,AC=BC=5,AB=8,AB⊥x轴,垂足为A,反比例函数y=(x>0)的图象经过点C,交AB于点D. (1)若OA=AB,求k的值. (2)若BC=BD,连接OC,求△OAC的面积. 6.(几何直观)如图,过原点O的直线与反比例函数y1=(k≠0)的图象交于A(1,2),B两点,一次函数y2=mx+b(m≠0)的图象过点A与反比例函数交于另一点C(2,n). (1)求反比例函数的解析式;当y1>y2时,根据图象直接写出x的取值范围. (2)在y轴上是否存在点M,使得△COM为等腰三角形 若存在,求出点M的坐标;若不存在,请说明理由. 【详解答案】 课堂达标 1.B　解析:在反比例函数y=-中,k=-6<0,图象在第二、第四象限.故选B. 2.一、第三　解析:设反比例函数的解析式为y=(k≠0).∵反比例函数的图象经过点(-3,-4),∴k=(-3)×(-4)=12. ∴函数的图象在第一、第三象限. 3.C　解析:A.∵(-3)×1=-3≠3,∴图象不经过点(-3,1).原说法错误,不符合题意;B.∵k=3>0,∴函数图象的两个分支分别位于第一、第三象限.在每一象限内,y随x的增大而减小.原说法错误,不符合题意;C.∵函数y=是反比例函数,∴图象不可能和x轴相交.原说法正确,符合题意;D.∵函数y=是反比例函数,∴图象是中心对称图形.原说法错误,不符合题意.故选C. 4.C　解析:∵反比例函数y=的图象经过点A(2,1),∴1=.∴k=2.∴该反比例函数的解析式为y=.故选C. 5.D　解析:如图,连接OA.∵AB∥y轴,∴△ABC的面积=△OAB的面积.∵2S△OAB=2×3=6,∴|k|=6.∵反比例函数图象在第二象限,∴k=-6.故选D. 6.y=　解析:设BC=a,AB=b,则点B的坐标为(-a,-b),AB·BC=ab=4.将点B(-a,-b)代入y=中,得k=xy=(-a)×(-b)=ab=4.∴反比例函数的解析式为y=. 7.解:(1)三　k>3 (2)由题意,设点A的坐标为(a,b). ∵点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,点C与点A关于原点O对称, ∴a>0,b>0,点B的坐标是(a,-b),点C的坐标是(-a,-b). ∴BC=a-(-a)=2a,AB=b-(-b)=2b. ∵△ABC的面积为4,∴×AB×BC=4. ∴×2a×2b=4.∴ab=2. ∵点A在反比例函数y= ... ...