期末评估测试卷（含答案） 2024-2025学年数学冀教版九年级下册

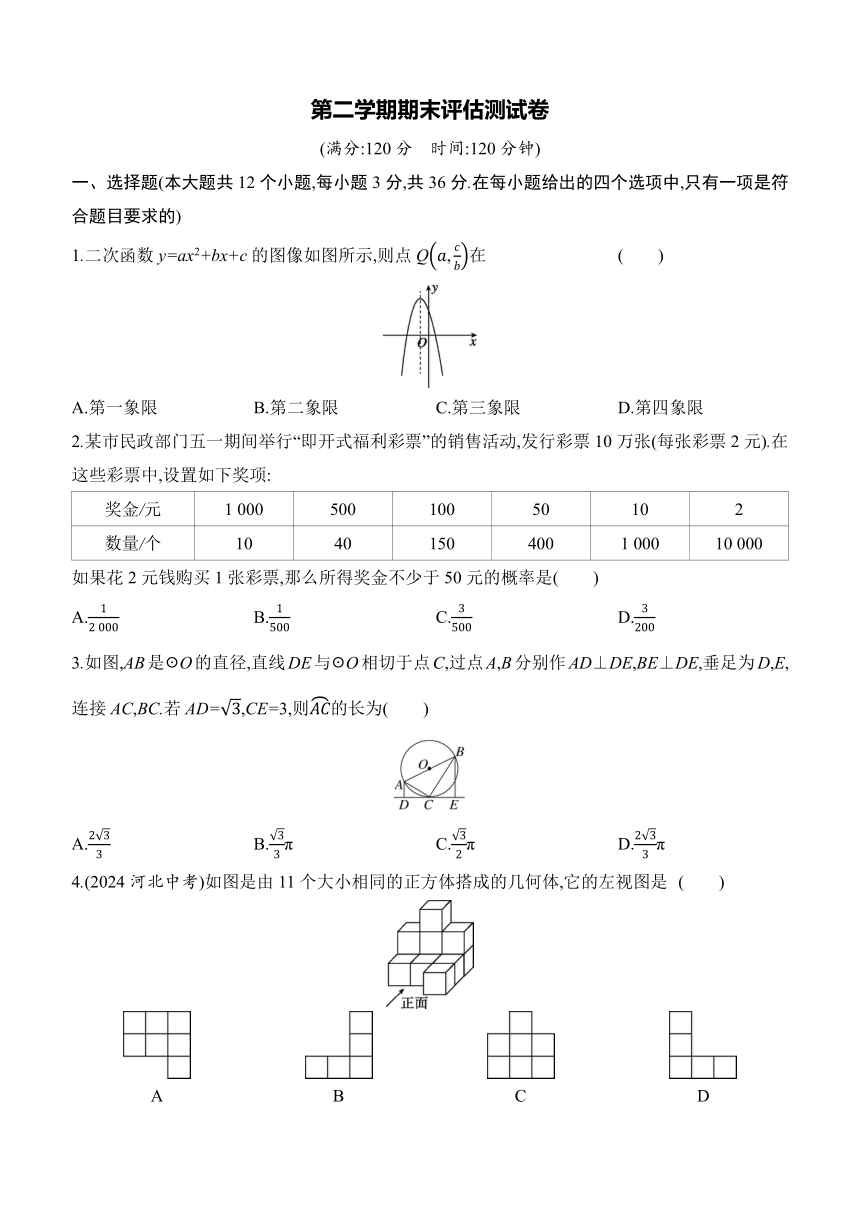
第二学期期末评估测试卷 (满分:120分　时间:120分钟) 一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.二次函数y=ax2+bx+c的图像如图所示,则点Q在 (　　) A.第一象限 B.第二象限 C.第三象限 D.第四象限 2.某市民政部门五一期间举行“即开式福利彩票”的销售活动,发行彩票10万张(每张彩票2元).在这些彩票中,设置如下奖项: 奖金/元 1 000 500 100 50 10 2 数量/个 10 40 150 400 1 000 10 000 如果花2元钱购买1张彩票,那么所得奖金不少于50元的概率是(　　) A. B. C. D. 3.如图,AB是☉O的直径,直线DE与☉O相切于点C,过点A,B分别作AD⊥DE,BE⊥DE,垂足为D,E,连接AC,BC.若AD=,CE=3,则的长为(　　) A. B.π C.π D.π 4.(2024河北中考)如图是由11个大小相同的正方体搭成的几何体,它的左视图是 (　　) A B C D 5.(2024广西中考)不透明袋子中装有白球2个,红球1个,这些球除了颜色外无其他差别.从袋子中随机取出1个球,取出白球的概率是(　　) A.1 B. C. D. 6.如图,Rt△ABC中,∠C=90°,AB=5,cos A=,以点B为圆心,r为半径作☉B,当r=3时,☉B与AC的位置关系是 (　　) A.相离 B.相切 C.相交 D.无法确定 7.如图,一块面积为60 cm2的三角形硬纸板(记为△ABC)平行于投影面时,在点光源O的照射下形成的投影是△A1B1C1.若OB∶BB1=2∶3,则△A1B1C1的面积是 (　　) A.90 cm2 B.135 cm2 C.150 cm2 D.375 cm2 8.(2024达州中考)抛物线y=-x2+bx+c与x轴交于两点,其中一个交点的横坐标大于1,另一个交点的横坐标小于1,则下列结论正确的是 (　　) A.b+c>1 B.b=2 C.b2+4c<0 D.c<0 9.(2024镇江中考)如图,小杰从灯杆AB的底部点B处沿水平直线前进到达点C处,他在灯光下的影长CD=3 m,然后他转身按原路返回到点B处,返回过程中小杰在灯光下的影长可以是 (　　) A.4.5 m B.4 m C.3.5 m D.2.5 m 10.已知实数a,b满足b-a=1,则代数式a2+2b-6a+7的最小值等于 (　　) A.5 B.4 C.3 D.2 11.如图,点A在半径为2的☉O上,过线段OA上的一点P(异于A点)作直线l,与☉O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图像大致是(　　) A B C D 12.已知二次函数y=ax2+bx+c(a≠0)的部分图像如图所示,图像经过点(0,2),其对称轴为直线x=-1.下列结论:①3a+c>0;②若点(-4,y1),(3,y2)均在二次函数图像上,则y1>y2;③关于x的一元二次方程ax2+bx+c=-1有两个相等的实数根;④满足ax2+bx+c>2的x的取值范围为-2”或“<”) 15.一个袋子中有若干个白球和绿球,它们除了颜色外都相同.随机从中摸一个球,恰好摸到绿球的概率是,则袋子中至少有　　　　个绿球. 16.如图,已知AB是☉O的直径,弦CD⊥AB于点E,过点B作BF∥CD交AD的延长线于点F. (1)BF与☉O的位置关系是　　　　. (2)若AD=3,cos∠BCD=,则AB=　　　　,CD=　　　　. 三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤) 17.(6分)周末清晨,小敏和父亲来到家附近的河堤散步,如图,梯形CDEF是露在地上的河堤一部分,河堤的一侧有一棵树,小敏想测量这棵树的高度.她和爸爸查询资料得知,河堤两侧的坡度iCD=1∶,iEF=∶1.某一时刻,在太阳光的照射下,树的影子一部分落在地面BC处,一部分落在斜坡CM处,M刚好是CD的中点,同时,小敏观察到此刻太阳光线与斜坡面EF所在的直线平行,经测量坡面CD=4 m,BC=7 m,请你帮小敏求出树AB的高度.(参考数据:≈1.7,结果保留 ... ...