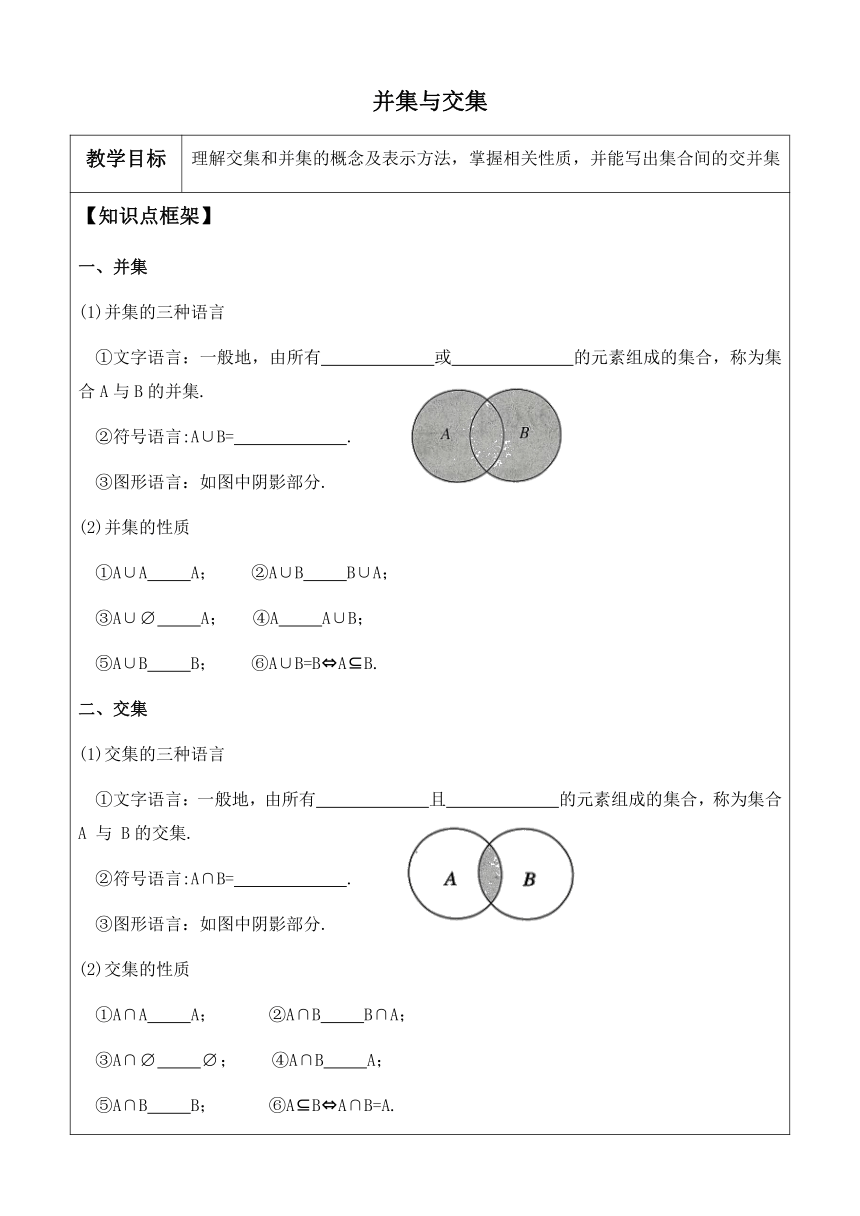
并集与交集 教学目标 理解交集和并集的概念及表示方法,掌握相关性质,并能写出集合间的交并集 【知识点框架】 一、并集 (1)并集的三种语言 ①文字语言:一般地,由所有 或 的元素组成的集合,称为集合A与B的并集. ②符号语言:A∪B= . ③图形语言:如图中阴影部分. (2)并集的性质 ①A∪A A; ②A∪B B∪A; ③A∪ A; ④A A∪B; ⑤A∪B B; ⑥A∪B=B A B. 二、交集 (1)交集的三种语言 ①文字语言:一般地,由所有 且 的元素组成的集合,称为集合A 与 B的交集. ②符号语言:A∩B= . ③图形语言:如图中阴影部分. (2)交集的性质 ①A∩A A; ②A∩B B∩A; ③A∩ ; ④A∩B A; ⑤A∩B B; ⑥A B A∩B=A. 思考: 1.并集的含义是什么 2.交集的含义是什么 【例题练习】 题型一:并集与交集的基本运算 例1.求下列两个集合的交集和并集. (1)A={1,3,4,6},B={2,3,5,6}; (2)A={x|x>-2},B={x|x≤3}; (3)A={x|-30},B={x|-1≤x≤2},则A∪B=( ) A.{x|x≥-1} B.{x|x≤2} C.{x|0a}. (1)若A∩B=,求a的取值范围; (2)若A∪B=R,求a的取值范围; (3)若1∈A∩B,求a的取值范围. 总结: (1)数形结合是高中数学中非常重要的思想方法. (2)常见的错误是丢掉a取端点时的值,如例3(1)写成a>2,例3(2)写成a<2,都是由于没有认真、仔细去考虑而造成的错误. 练习: 1.设A={x|a≤x≤a+3},B={x|x<-1或x>5},当a为何值时, (1)A∩B=;(2)A∩B≠;(3)A∩B=A. 【课后巩固】 1.已知A={1,2,3,4},B={2,3,4,5},则A∪B=( ) A.{1,2,3,4,5} B.{2,3,4} C.{1,2,4} D.{2,3,5} 2.设集合M={1,2,4,8},N={x|x是2的倍数},则M∩N=( ) A.{2,4} B.{1,2,4} C.{2,4,8} D.{1,2,8} 3.设M={3,a},N={1,2},M∩N={2},则M∪N=( ) A.{1,2} B.{1,3} C.{1,2,3} D.{1,2,3,a} 4.已知集合 A={1,3,},B={1,m},A∪B=A,则m=( ) A.0或 B.0或3 C.1或 D.1或3 5.若A={x|x=2k,k∈Z},B={x|x=4k+2,k∈Z},则A∩B= . 【课外拓展】 1.用Venn图表示两个集合的交集,所有可能的关系有以下五种 (1)若A B,则A∩B=A,如图1. (2)若B A,则A∩B=B,如图2. (3)若A=B,则A∩B=A=B,如图3. (4)若两个集合有公共元素,但互不包含,A∩B≠,如图 4. (5)若两个集合无公共元素,A∩B=,如图5. 2.用 Venn 图表示两个集合的并集,所有可能的关系如下图 (1)若A B,则A∪B=B,如图 1. (2)若B A,则A∪B=A,如图2. (3)若A=B,则A∪B=A=B,如图3. (4)若A与B有公共元素,但互不包含,则A∪B 如图 4. (5)若A与B没有公共元素,则A∪B如图5. ... ...
~~ 您好,已阅读到文档的结尾了 ~~