专项训练06　常考解直角三角形模型 学案（含答案） 2025年中考数学一轮专题复习（河北）

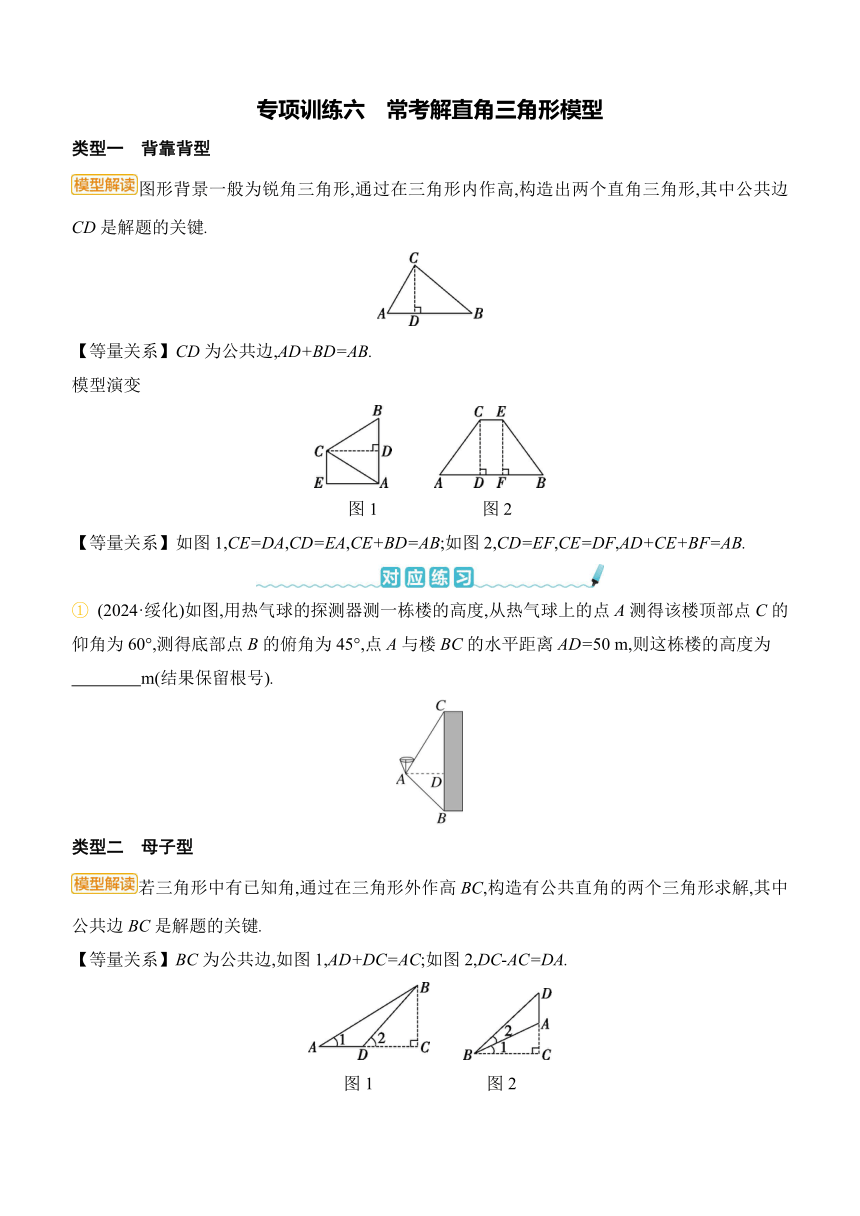
专项训练六　常考解直角三角形模型 类型一　背靠背型 图形背景一般为锐角三角形,通过在三角形内作高,构造出两个直角三角形,其中公共边CD是解题的关键. 【等量关系】CD为公共边,AD+BD=AB. 模型演变 图1　 　图2 【等量关系】如图1,CE=DA,CD=EA,CE+BD=AB;如图2,CD=EF,CE=DF,AD+CE+BF=AB. ① (2024·绥化)如图,用热气球的探测器测一栋楼的高度,从热气球上的点A测得该楼顶部点C的仰角为60°,测得底部点B的俯角为45°,点A与楼BC的水平距离AD=50 m,则这栋楼的高度为 　　　　m(结果保留根号). 类型二　母子型 若三角形中有已知角,通过在三角形外作高BC,构造有公共直角的两个三角形求解,其中公共边BC是解题的关键. 【等量关系】BC为公共边,如图1,AD+DC=AC;如图2,DC-AC=DA. 图1　　 图2 模型演变1 图3　　 图4 【等量关系】如图3,DF=EC,DE=FC,BF+DE=BC,AE+DF=AC;如图4,AF=CE,AC=FE,BC+AF=BE. 模型演变2 图5　 　图6　 　图7 【等量关系】如图5,BE+EC=BC;如图6,EC-BC=BE;如图7,AC=FG,AF=CG,AD+DC=FG,BC+AF =BG. 模型演变3 图8　　 图9 【等量关系】如图8,BC=FG,BF=CG,AC+BF=AG,EF+BC=EG;如图9,BC=FG,BF=CG,EF+BC= EG,BD+DF=BF,AC+BD+DF=AG. ② (2024·安徽)科技社团选择学校游泳池进行一次光的折射实验,如图,光线自点B处发出,经水面点E折射到池底点A处.已知BE与水平线的夹角α=36.9°,点B到水面的距离BC=1.20 m,点A处水深为1.20 m,到池壁的水平距离AD=2.50 m.点B,C,D在同一条竖直线上,所有点都在同一竖直平面内.记入射角为β,折射角为γ,求的值(精确到0.1,参考数据:sin 36.9°≈0.60,cos 36.9°≈0.80,tan 36.9°≈0.75). ③ (2024·辽宁)如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图2,此时测得点A到BC所在直线的距离AC=3 m,∠CAB=60°,停止位置示意图如图3,此时测得∠CDB=37°(点C,A,D在同一直线上,且直线CD与地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变. (1)求AB的长. (2)求物体上升的高度CE(结果精确到0.1 m). (参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73) 图1　 图2　 图3 类型三　拥抱型 分别解两个直角三角形,其中公共边BC是解题的关键. 【等量关系】BC为公共边. 模型演变 图1　 图2 图3 【等量关系】如图1,BF+FC+CE=BE;如图2,BC+CE=BE;如图3,AB=GE,AG=BE,BC+CE=AG, DG+AB=DE. ④ (2024·巴中)某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡BE的坡度i=1∶,BE=6 m,在B处测得电线塔CD顶部D的仰角为45°,在E处测得电线塔CD顶部D的仰角为60°. (1)求点B离水平地面的高度AB. (2)求电线塔CD的高度(结果保留根号). 【详解答案】 对应练习 1.(50+50)　解析:由题意,得AD⊥BC, 在Rt△ACD中,∠CAD=60°,AD=50 m, ∴CD=AD·tan 60°=50×=50(m). 在Rt△ABD中,∠BAD=45°, ∴BD=AD·tan 45°=50×1=50(m), ∴BC=BD+CD=(50+50)m, ∴这栋楼的高度为(50+50)m. 2.解:如图,过点E作EH⊥AD于点H, 由题意可知,∠CEB=α=36.9°, EH=1.20 m, ∴CE=≈=1.60(m), ∴AH=AD-CE=2.50-1.60=0.90(m), ∴AE===1.50(m), ∴sin γ==0.60. ∵sin β=sin∠CBE==cos∠CEB=cos α≈0.80, ∴≈1.3. 3.解:(1)如题图2,在Rt△ABC中,AC=3 m,∠CAB=60°, ∴∠ABC=30°, ∴AB=2AC=6 m, 故AB的长为6 m. (2)在Rt△ABC中,AB=6 m,AC=3 m, 根据勾股定理,得BC= =3(m). 在Rt△BCD中,∠CDB=37°, ∵sin∠CDB=,即≈0.60, ∴BD≈=8.65(m), ∴CE=BD-BA=8.65-6=2.65≈2.7(m), 故物体上升的高度CE约为2.7 m. 4.解:(1)由题意,得BA⊥AE, ∵斜坡BE的坡度i=1∶,∴. 在Rt△ABE中,tan∠BEA=, ∴∠BEA=30°. ∵BE=6 m, ∴AB=BE=×6=3(m),AE=AB=×3=3(m), ∴点B离水平地面的高度AB为3 ... ...