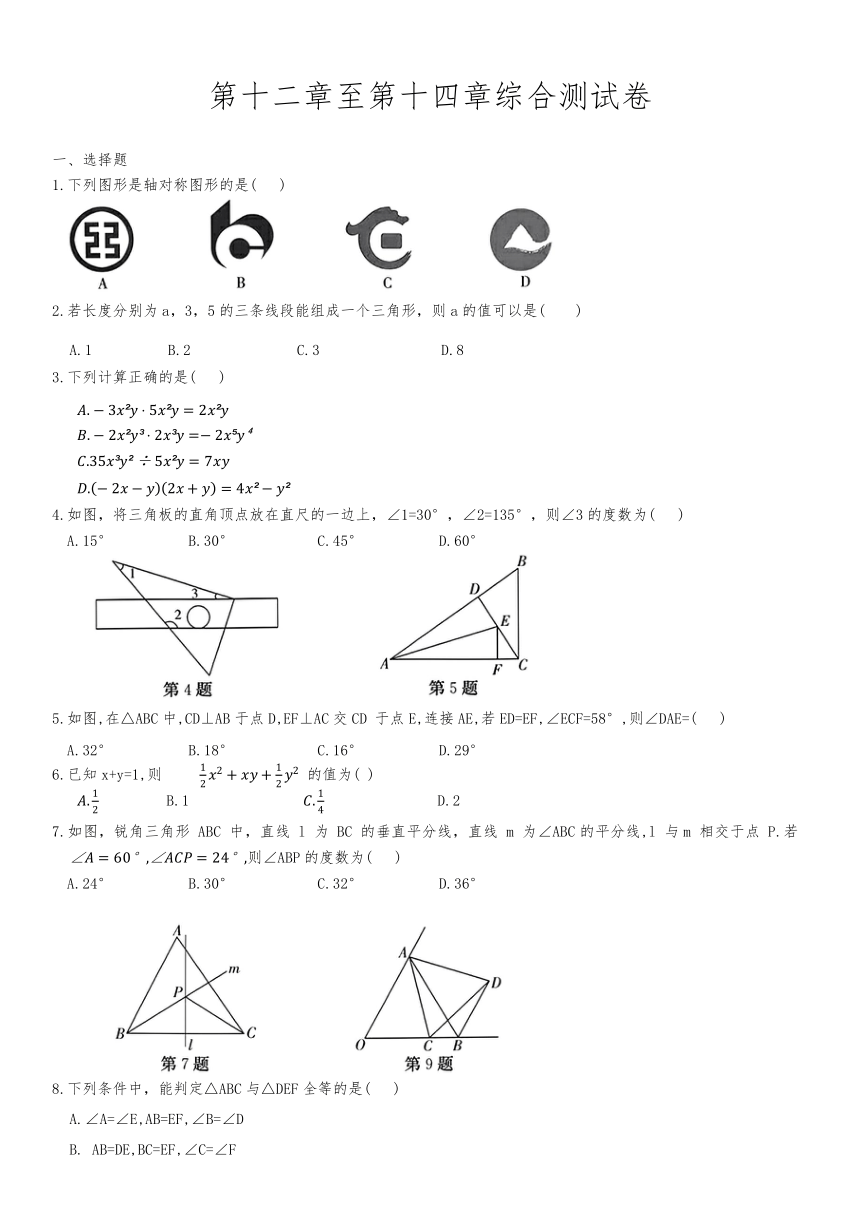
第十二章至第十四章综合测试卷 一、选择题 1.下列图形是轴对称图形的是( ) 2.若长度分别为a,3,5的三条线段能组成一个三角形,则a的值可以是( ) A.1 B.2 C.3 D.8 3.下列计算正确的是( ) 4.如图,将三角板的直角顶点放在直尺的一边上,∠1=30°,∠2=135°,则∠3的度数为( ) A.15° B.30° C.45° D.60° 5.如图,在△ABC中,CD⊥AB于点D,EF⊥AC交CD 于点E,连接AE,若ED=EF,∠ECF=58°,则∠DAE=( ) A.32° B.18° C.16° D.29° 6.已知x+y=1,则 的值为( ) B.1 D.2 7.如图,锐角三角形 ABC 中,直线 l 为 BC 的垂直平分线,直线 m 为∠ABC的平分线,l 与m 相交于点 P.若 则∠ABP的度数为( ) A.24° B.30° C.32° D.36° 8.下列条件中,能判定△ABC与△DEF全等的是( ) A.∠A=∠E,AB=EF,∠B=∠D B. AB=DE,BC=EF,∠C=∠F C. AB=DE,BC=EF,∠A=∠E D.∠A=∠D,AB=DE,∠B=∠E 9.如图,在△AOB中,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB方向移动,以AC为边向右侧作等边△ACD,连接BD,则下列结论不一定成立的是( ) A. OC=BD B.∠OBD=120° C. OA∥BD D. AB平分∠OAD 10.我们知道下面的结论:若 ,且a≠1),则m=n.利用这个结论解决下列问题:设2"=3,2"=6,2'=12,下列关系式正确的是( ) B. m+n=2p C. m+p=2n D. p+n=2m 二、填空题 11.分解因式:am -9a= . 12.若一个多边形的内角和等于它的外角和,则这个多边形的边数为 . 13.已知有两个三角形全等,若一个三角形三边的长分别为3,5,7,另一个三角形三边的长分别为3,3a—2b,a+2b,则a+b= . 14.如图,点 P 是∠AOB外的点,点 M,N分别是∠AOB 两边上的点,点P 关于OA 的对称点Q恰好落在线段MN 上,点 P 关于OB 的对称点R落在MN 的延长线上.若PM=2.5cm,PN=3cm,MN=4cm,则线段 QR 的长为 . 15.如图,在Rt△ABC中,∠C=90°,∠B=30°,以点 A为圆心,任意长为半径画弧分别交AB,AC于点M,N,再分别以点 M,N为圆心,大于 的长为半径画弧,两弧交于点 P,连接AP 并延长交BC 于点D,则下列说法:①AD平分 ;③点 D在AB 的垂直平分线上;( 其中正确的个数是 . 三、解答题 16.(8分)如图,在 中, 的外角 的平分线BE 交AC 的延长线于点 E. (1)求 的度数; (2)过点D作 ,交AC的延长线于点F.求 的度数. 17.(9分)化简: (a-2b+3c)(a+2b-3c). 18.(9分)如图,已知△ABC的顶点分别为A(-2,2),B(-4,5),C(-5, 1)和直线m(直线m上各点的横坐标都为1). (1)作出△ABC关于x轴对称的图形 并写出点 的坐标: (2)作出△ABC关于y轴对你的图形. 并写出点 的坐标: (3)若点P(a,b)是△ABC内部一点,则点 P关于直线m 对称的点的坐标是 . 19.(9分)在△ABC中,AB=AC,AC边上的中线BD 把△ABC的周长分为21厘米和12厘米两部分,求△ABC各边的长. 20.(9分)如图,△ABC是等边三角形,点 D,E分别在边BC,AC上=BD,连接DE,过点E作EF⊥DE,交线段BC的延长线于点 F. (1)求证:CE=CF. (2)若 求线段 DF的长. 21.(10分)如图,已知 ,D是直线AB 上的点,. 过点A作 并截取 ,连接DC,DF,CF,判断, 的形状并证明. 22.(10分)整式的乘法与因式分解是有理数运算的自然延伸,也是代数知识的基本内容,请利用相关知识解决下面的问题: (1)化简计算:( (2)在(1)题结果的基础上,增加一个单项式,使新得到的多项式能运用完全平方公式进行因式分解,请写出所有这样的单项式,并进行因式分解; (3)试说明两个连续奇数的平方差能够被8整除. 23.(11分)问题背景:如图1,已知AM∥BN,∠BAM,∠ABN的平分线交于点E,过点 E的直线交射线AM 于点C,交射线 BN于点D,探究图中AC,BD与AB 之间的数量关系. (1)小王同学探究此问题的方法:延长AE 交 BN 于点 F,先证明 再证明 然后证明 ,可得出结论,他的结论应是 . 探索延伸:如图2,已知. 的平分线交于点E,过点 E 的直线交射线 AM 的反向延长线 ... ...
~~ 您好,已阅读到文档的结尾了 ~~