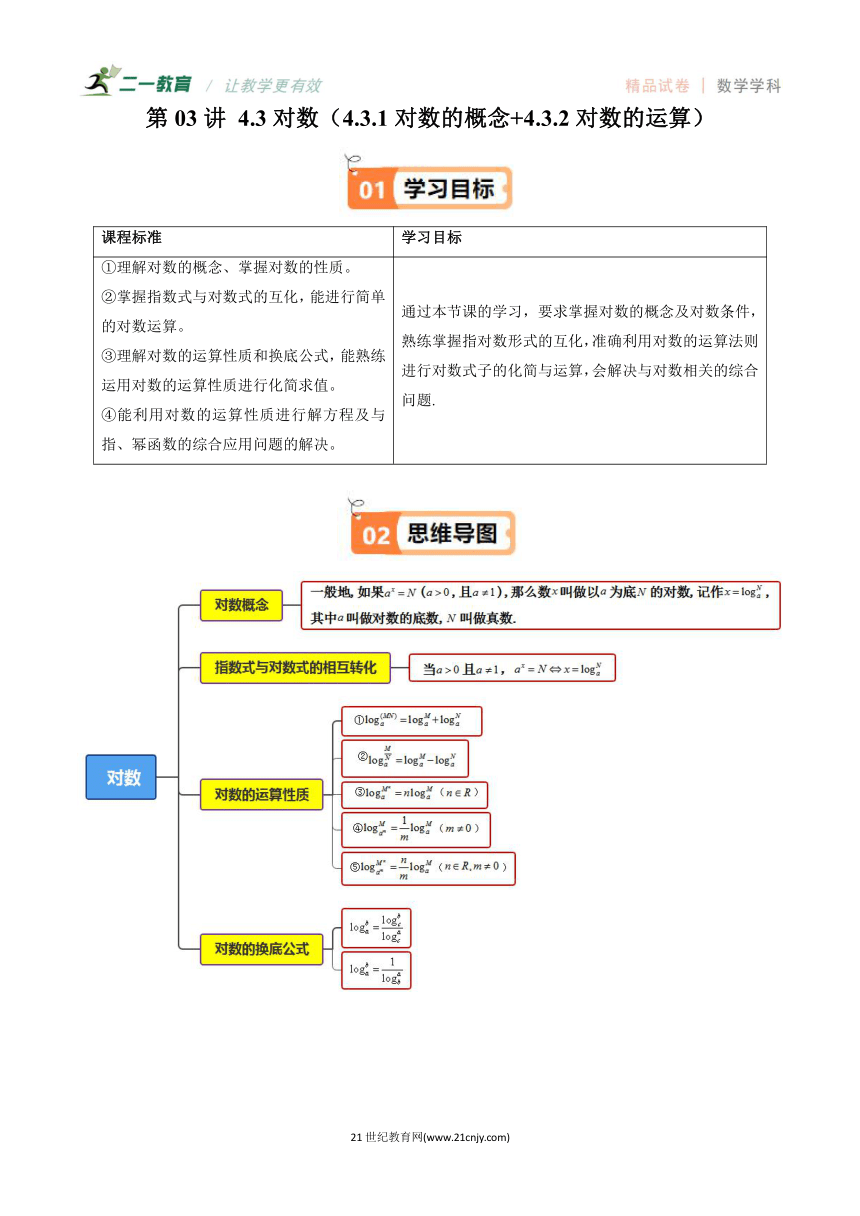
第03讲 4.3对数(4.3.1对数的概念+4.3.2对数的运算) 课程标准 学习目标 ①理解对数的概念、掌握对数的性质。 ②掌握指数式与对数式的互化,能进行简单的对数运算。 ③理解对数的运算性质和换底公式,能熟练运用对数的运算性质进行化简求值。 ④能利用对数的运算性质进行解方程及与指、幂函数的综合应用问题的解决。 通过本节课的学习,要求掌握对数的概念及对数条件,熟练掌握指对数形式的互化,准确利用对数的运算法则进行对数式子的化简与运算,会解决与对数相关的综合问题. 知识点01:对数概念 1、对数的概念:一般地,如果(,且),那么数叫做以为底的对数,记作,其中叫做对数的底数,叫做真数. 特别的:规定,且的原因: ①当时,取某些值时,的值不存在,如:是不存在的. ②当时,当时,的值不存在,如:是不成立的;当时,则的取值时任意的,不是唯一的. ③当时,当,则的值不存在;当时,则的取值时任意的,不是唯一的. 【即学即练1】(2024高一·全国·专题练习)在中,实数的取值范围是( ) A.或 B.或 C. D. 2、常用对数与自然对数 ①常用对数:将以10为底的对数叫做常用对数,并把记为 ②自然对数:是一个重要的常数,是无理数,它的近似值为2.718 28.把以为底的对数称为自然对数,并把记作 说明:“”同+、-、×等符号一样,表示一种运算,即已知一个底数和它的幂求指数的运算,这种运算叫对数运算,不过对数运算的符号写在数的前面. 知识点02:指数式与对数式的相互转化 当且, 知识点03:对数的性质 ①负数和零没有对数. ②对于任意的且,都有,,; ③对数恒等式: (且) 【即学即练2】(2024高二上·福建·学业考试)若,,则等于( ) A. B. C. D. 知识点04:对数的运算性质 当且,, ① ② ③() ④() ⑤() 【即学即练3】(23-24高二下·北京·阶段练习) . 知识点05:对数的换底公式 换底公式:(且,,,且) 特别的: 【即学即练4】(23-24高一下·上海嘉定·阶段练习) 题型01对数概念判断与求值 【典例1】(23-24高一上·贵州贵阳·阶段练习)使式子有意义的的取值范围是( ) A. B. C.且 D., 【典例2】(23-24高一上·全国·课后作业)若有意义,则实数k的取值范围是 . 【典例3】(23-24高一·全国·课后作业)已知,则x的值为 . 【变式1】(23-24高一上·福建福州·期中)使式子有意义的x的取值范围是( ) A. B. C. D. 【变式2】(23-24高一上·上海浦东新·期中)若代数式有意义,则实数的取值范围是 . 【变式3】(23-24高一·全国·课后作业)若函数是对数函数,则 . 题型02指数式与对数式相互转换 【典例1】(23-24高一上·福建厦门·期末)已知,则( ) A.2 B. C.3 D.4 【典例2】(23-24高一上·新疆乌鲁木齐·期末)将化成指数式可表示为( ) A. B. C. D. 【典例3】(2023高一上·全国·专题练习)将下列指数式、对数式互化. (1); (2); (3); (4). 【变式1】(23-24高一上·广西河池·期末)若,则的值为( ) A.2 B.3 C.5 D.8 【变式2】(23-24高一上·广东深圳·期末)已知,,则 . 【变式3】(22-23高一·全国·随堂练习)将下列对数式改写为指数式: (1); (2); (3); (4). 题型03对数的运算 【典例1】(23-24高一下·湖北·阶段练习) . 【典例2】(23-24高一下·山西大同·阶段练习)化简下列各式: (1); (2). 【典例3】(23-24高一上·广东中山·阶段练习)计算下列各式的值; (1); (2) 【变式1】(23-24高一上·广东茂名·期中)计算: . 【变式2】(23-24高一下·黑龙江哈尔滨·开学考试)求值: (1); (2). 【变式3】(23-24高一上·安徽·期末)计算: (1); (2). 题型04对数运算性质的应用 【典例1】(2024·四川·模拟预测)若实数,,满足且,则 ... ...
~~ 您好,已阅读到文档的结尾了 ~~