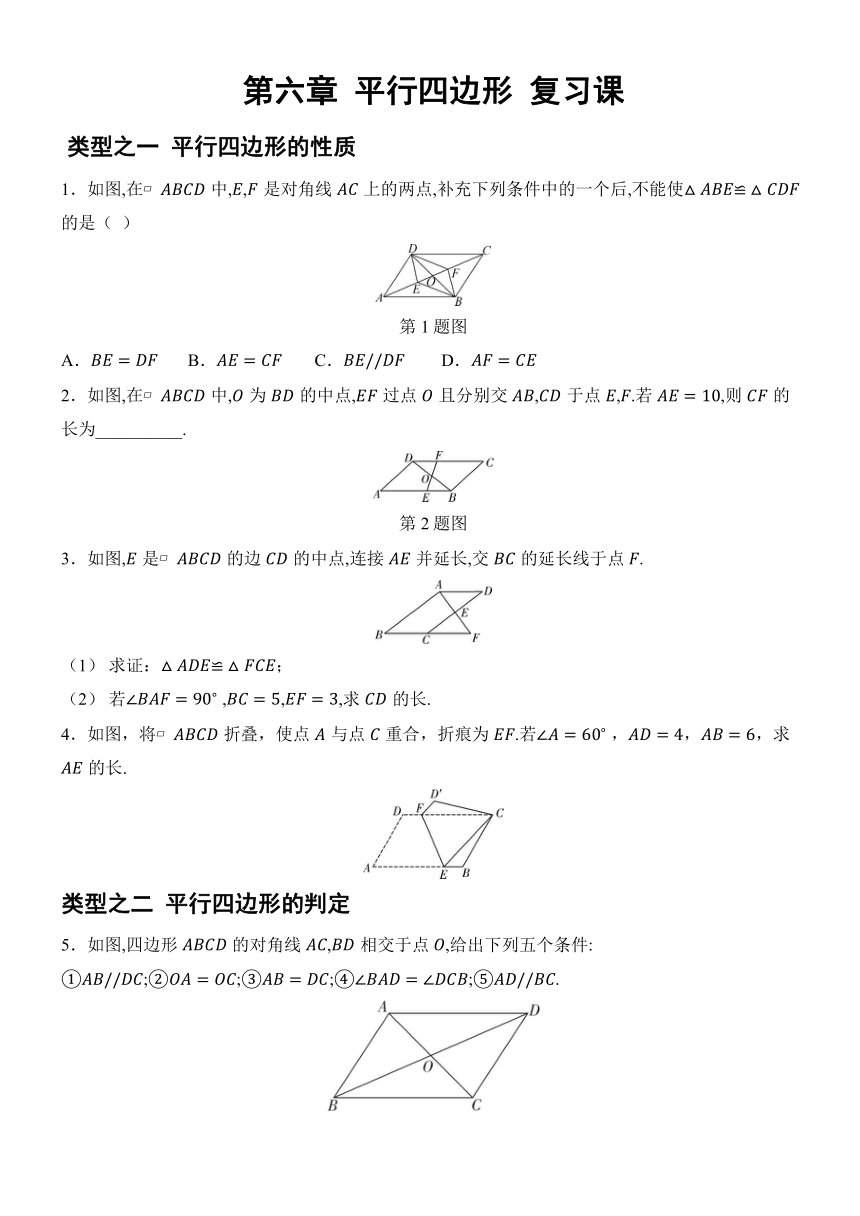
第六章 平行四边形 复习课 类型之一 平行四边形的性质 1.如图,在中,,是对角线上的两点,补充下列条件中的一个后,不能使的是( ) 第1题图 A. B. C. D. 2.如图,在中,为的中点,过点且分别交,于点,.若,则的长为_____. 第2题图 3.如图,是的边的中点,连接并延长,交的延长线于点. (1) 求证:; (2) 若 ,,,求的长. 4.如图,将折叠,使点与点重合,折痕为.若 ,,,求的长. 类型之二 平行四边形的判定 5.如图,四边形的对角线,相交于点,给出下列五个条件: ;;;;. (1) 从以上五个条件中任意选取两个条件,能推出四边形是平行四边形的有(用序号表示):①与⑤、_____; (2) 对由以上五个条件中任意选取两个条件,不能推出四边形是平行四边形的,请选取一种情形举出反例说明. 6.[2024深圳模拟]如图,,是对角线上的两点,. (1) 求证:四边形是平行四边形; (2) 若的面积为6, ,,则的长是_____. 7.如图,将的边延长至点,使,连接,是边的中点,连接. (1) 求证:四边形是平行四边形. (2) 若,, ,求的长. 类型之三 三角形的中位线 8.如图,在中, ,,,是边上一点,为边上的动点,,分别为,的中点,则的最小值是_____. 9.如图,在中,,分别是边,的中点,连接,,点在的延长线上,且,连接,求证:四边形是平行四边形. 类型之四 多边形的内角和与外角和 10.[2024宜春模拟]某同学在进行多边形的内角和的计算时,求得的内角和为 .当发现错了之后,重新检查,发现是多加了一个内角.问:多加的这个内角的度数是多少?这个多边形是几边形? 11.如图,求的度数. 第六章复习课 类型之一 平行四边形的性质 1.A 2. 3.(1) 证明: 四边形是平行四边形, ,, ,. 是的中点,. 在和中, . (2) 解:, . , . 四边形是平行四边形, , . 又由(1)知, . 4.解:如答图,过点作于点,则 . 第4题答图 四边形是平行四边形,,, , ,,. 设,则,. 由折叠可知,. ,, 解得,的长为. 类型之二 平行四边形的判定 5.(1) ①与②、①与③、①与④、②与⑤、④与⑤ (2) 解:③与⑤不能推出四边形是平行四边形,反例:等腰梯形(答案不唯一). 6.(1) 证明: 四边形是平行四边形,,,. 又,. 在和中,,. 又, 四边形是平行四边形. (2) 7.(1) 证明: 四边形是平行四边形,,,即. 是的中点,. ,,. 又, 四边形是平行四边形. (2) 解:的长为. 类型之三 三角形的中位线 8. 9.证明:,分别是边,的中点, ,. , ,且. 四边形是平行四边形. 类型之四 多边形的内角和与外角和 10.解:设这个多边形的边数为,根据题意可知,多加的内角为 . 则解得. 为正整数,. 多加的内角为 . 故多加的这个内角是 ,这个多边形是八边形. 11.解:是的外角,. 是的外角,. . ... ...
~~ 您好,已阅读到文档的结尾了 ~~