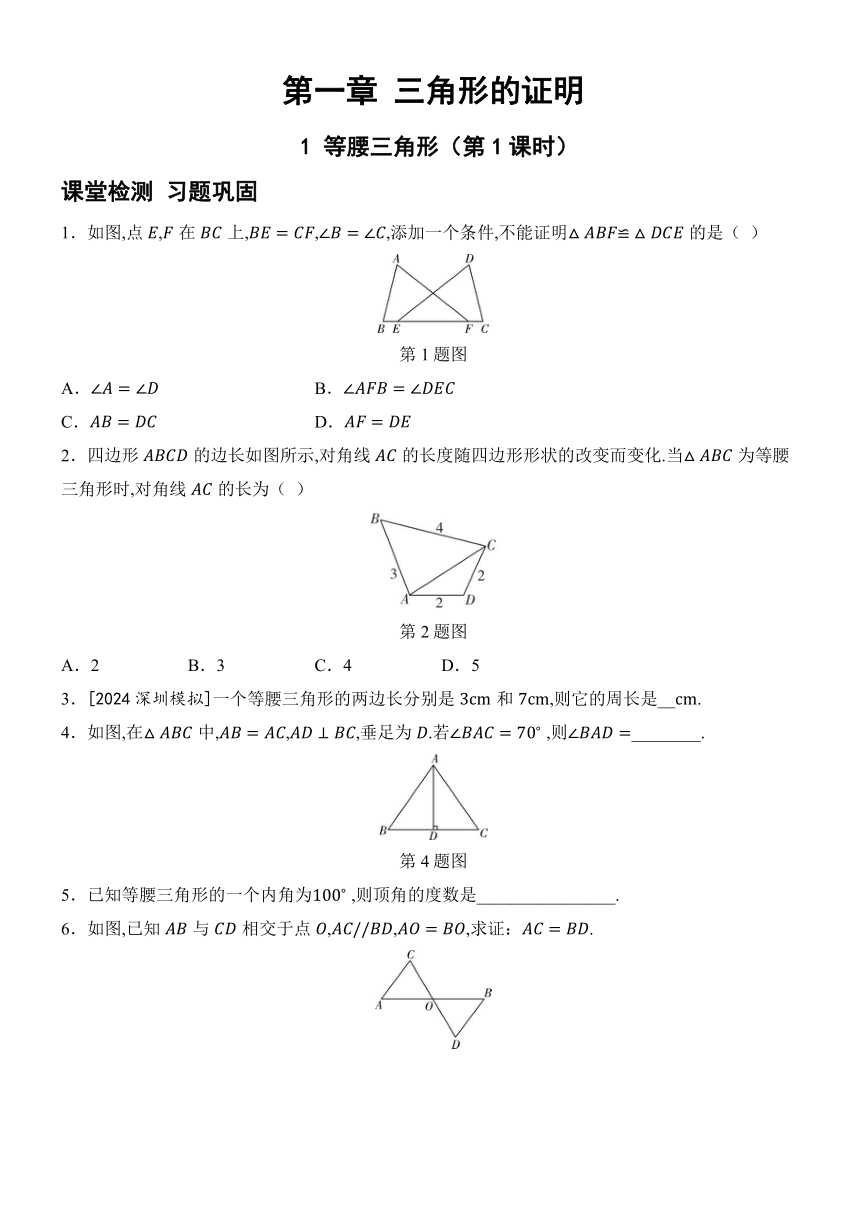
第一章 三角形的证明 1 等腰三角形(第1课时) 课堂检测 习题巩固 1.如图,点,在上,,,添加一个条件,不能证明的是( ) 第1题图 A. B. C. D. 2.四边形的边长如图所示,对角线的长度随四边形形状的改变而变化.当为等腰三角形时,对角线的长为( ) 第2题图 A.2 B.3 C.4 D.5 3.[2024深圳模拟]一个等腰三角形的两边长分别是和,则它的周长是__. 4.如图,在中,,,垂足为.若 ,则_____. 第4题图 5.已知等腰三角形的一个内角为 ,则顶角的度数是_____. 6.如图,已知与相交于点,,,求证:. 1 等腰三角形(第2课时) 课堂检测 习题巩固 1.[2024深圳模拟]已知为等边三角形,则的度数是( ) A. B. C. D. 2.[2023上海]下列说法中,错误的是( ) A.等腰三角形两腰上的高相等 B.等腰三角形两腰上的中线相等 C.等腰三角形两底角的平分线相等 D.等腰三角形高、中线和角平分线重合 3.如图,在等边三角形中,,分别是,边上的高,且,相交于点,则的度数为_____. 第3题图 4.如图,直线,过等边三角形的顶点和,且, ,则的度数为_____. 第4题图 5.如图,是等边三角形的中线,以点为圆心,的长为半径画弧,交的延长线于点,连接.求证:. 1 等腰三角形(第3课时) 课堂检测 习题巩固 1.如图,在等腰中,为的平分线, ,,,则的周长为( ) 第1题图 A. B. C. D. 2.如图,在中,,, ,则图中等腰三角形共有( ) 第2题图 A.3个 B.4个 C.5个 D.6个 3.如图,一艘船从处观测海岛在北偏东 方向,上午11时该船从处出发,以的速度沿正北方向航行到处,再观测海岛在北偏东 方向,且此时该船距离海岛,则该船到达处的时间为__时. 第3题图 4.以下是用反证法证明:等腰三角形的两底角必为锐角.请将过程补充完整. 证明:①假设等腰三角形的底角,都是直角,则_____, 从而_____ , 这与_____矛盾; ②假设等腰三角形的底角,都是钝角, 则_____,从而_____, 这与_____矛盾. 综上所述,假设①②_____, ,只能为____. 等腰三角形的两底角必为锐角. 5.[2024平顶山模拟]如图,在中,,是通过如图的作图痕迹作图而得,,交于点. (1) 求证:; (2) 若 ,则的度数是_____. 1 等腰三角形(第4课时) 课堂检测 习题巩固 1.下列条件中,不能得到等边三角形的是( ) A.有两个内角是 的三角形 B.三边都相等的三角形 C.有一个角是 的等腰三角形 D.有两个外角相等的等腰三角形 2.2023年5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为 ,腰长为,则底边上的高是( ) 第2题图 A. B. C. D. 3.如图,在中, , ,是斜边上的高,,则的长是( ) 第3题图 A. B. C. D. 4.如图,一棵树在一次强台风中于离地面处折断倒下,倒下部分与地面成 夹角,这棵树在折断前的高度为__. 第4题图 5.如图,,,.求证:是等边三角形. 1 等腰三角形(第1课时) 课堂探究 例题点拨 类型之一 全等三角形的判定公理和性质公理的应用 例1 证明:, . , ,即. 在和中, . . 『本题通过证明三角形全等得到对应边相等,综合考查了全等三角形的判定和性质.』 类型之二 等腰三角形的性质证明 例2 证明:方法一: 点是的中点,. 在和中,,. 方法二、方法三的证明略. 类型之三 等腰三角形的性质及三角形内角和定理的综合运用 例3 解: ,, . 是的中点,,是的垂直平分线, , , . 课堂检测 习题巩固 1.D 2.B 3.17 4. 5. 6.证明:. ,. 在和中, , . 1 等腰三角形(第2课时) 课堂探究 例题点拨 类型之一 证明等腰三角形的有关结论 例1 证明:,,, ,. 在和中, . 【变式】 证明:,, . 在和中, . . 类型之二 等边三角形的性质 例2 证明:是等边三角形, , , . 在和中, . 『等边三角形的三个角都相等,三条边都相等,所 ... ...
~~ 您好,已阅读到文档的结尾了 ~~