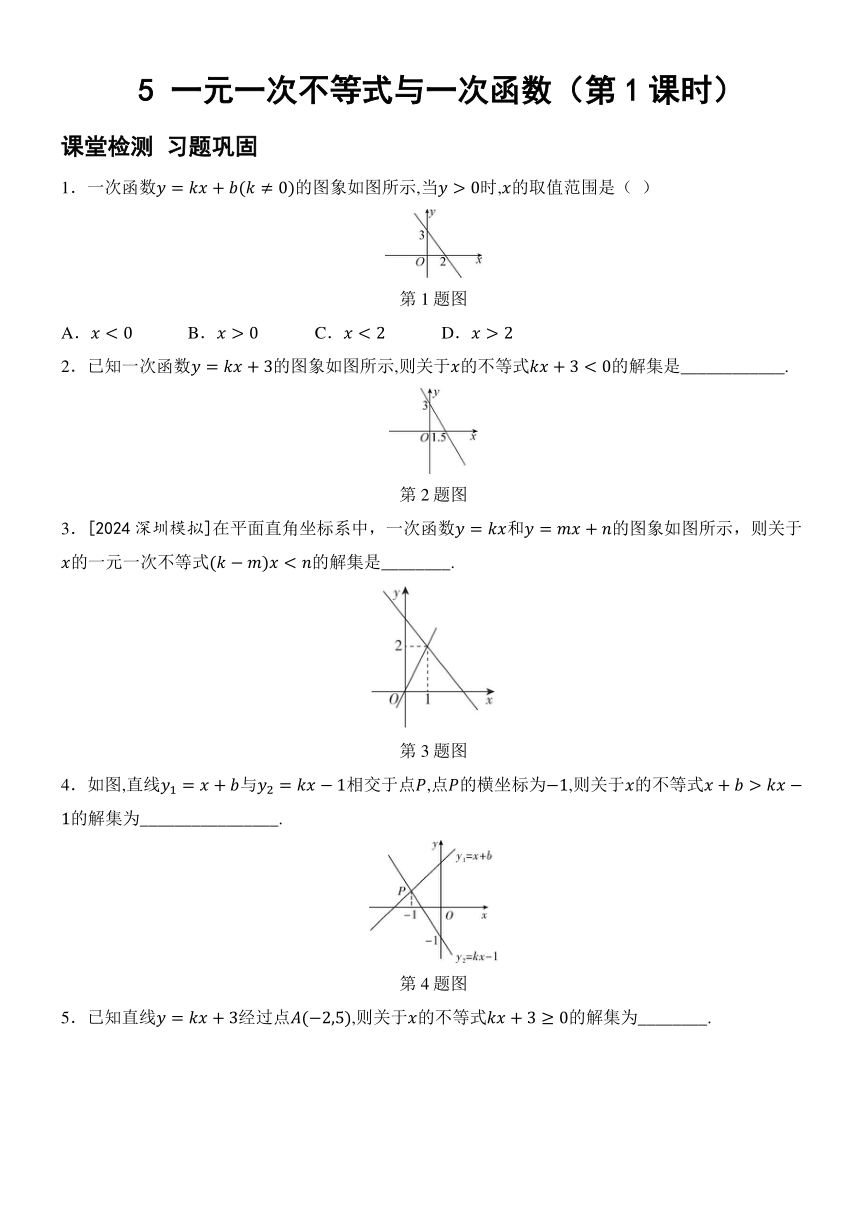
5 一元一次不等式与一次函数(第1课时) 课堂检测 习题巩固 1.一次函数的图象如图所示,当时,的取值范围是( ) 第1题图 A. B. C. D. 2.已知一次函数的图象如图所示,则关于的不等式的解集是_____. 第2题图 3.[2024深圳模拟]在平面直角坐标系中,一次函数和的图象如图所示,则关于的一元一次不等式的解集是_____. 第3题图 4.如图,直线与相交于点,点的横坐标为,则关于的不等式的解集为_____. 第4题图 已知直线经过点,则关于的不等式的解集为_____. 5 一元一次不等式与一次函数(第2课时) 课堂检测 习题巩固 1.如图,反映了某公司的销售收入与销售量之间的关系,反映了该公司产品的销售成本与销售量之间的关系,当该公司赢利(收入大于成本)时,销售量是( ) A.小于 B.大于 C.小于 D.大于 2.[2024九江模拟]已知某服装厂现有布料,现计划用这种布料生产,两种型号的时装共80套.已知做一套型号的时装需用布料,可获利100元;做一套型号的时装需用布料,可获利45元.设生产型号的时装套数为,用这批布料生产两种型号的时装所获得的总利润为元. (1) 求与之间的函数表达式. (2) 当生产型号的时装多少套时,才能使该厂所获总利润最大?最大总利润是多少? 3.为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额(元)与骑行时间之间的函数关系.根据图象解答下列问题. (1) 求手机支付金额与骑行时间之间的函数表达式; (2) 李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算. 5 一元一次不等式与一次函数(第1课时) 课堂探究 例题点拨 类型之一 一元一次不等式与一次函数的关系 『我们可以通过解不等式(方程)来求函数值的大小问题,也可以直接利用函数图象观察得出结论.』 例1 (1) 解: 当时,; 当时,; 当时,. 对于函数, 例1 (1) 当时,. (2) 当时,. (3) 当时,. 类型之二 利用函数图象解不等式 『解关于 的不等式 可以转化为:(1)当自变量 取哪些值时,直线 上的点在 轴的上方;(2)当 取哪些值时,直线 上的点在直线 上相应的点的上方.(不等号为“ ”时是同样的解题方法)』 例2 C 类型之三 一元一次不等式与一次函数的应用 例3 (1) 解:根据题意,得,,即,与之间的函数关系式分别是,. 函数图象如答图. 例3答图 (2) ,解得. 答:当时,弟弟跑在哥哥的前面. (3) 令,解得;令,解得, , 小新先跑过. 令,解得;令,解得, , 小高先到达终点. 课堂检测 习题巩固 1.C 2. 3. 4. 5. 5 一元一次不等式与一次函数(第2课时) 课堂探究 例题点拨 类型之一 利用函数值的大小比较选择方案 例1 解:当购买乙物品的数量超过200套不足450套时,选择优惠方案一更合算;当购买乙物品的数量等于450套时,选择优惠方案一和优惠方案二所需费用相同,两种方案一样合算;当购买乙物品的数量超过450套时,选择优惠方案二更合算.理由如下: 设购买乙物品套,则选择优惠方案一所需费用为元,选择优惠方案二所需费用为元. 若,则, 当时,选择优惠方案一更合算; 若,则, 当时,选择优惠方案一和优惠方案二所需费用相同,两种方案一样合算; 若,则, 当时,选择优惠方案二更合算. 【变式】 (1) 解:根据题意,设,且图象过点, 则有,解得, . 根据题意,得. (2) 当时,, 解得; 当时,, 解得; 当时,, 解得. 当租车时间为时,选择甲、乙公司一样合算;当租车时间小于时,选择乙公司更合算;当租车时间大于时,选择甲公司更合算. 类型之二 利用一次函数的性质选择方案 『在生产生活中,经常会涉及求最大利润,最省费用等问题,这类问题经常利用函数来解答,其步骤一般是:先列出关于自变量的方程 ... ...
~~ 您好,已阅读到文档的结尾了 ~~