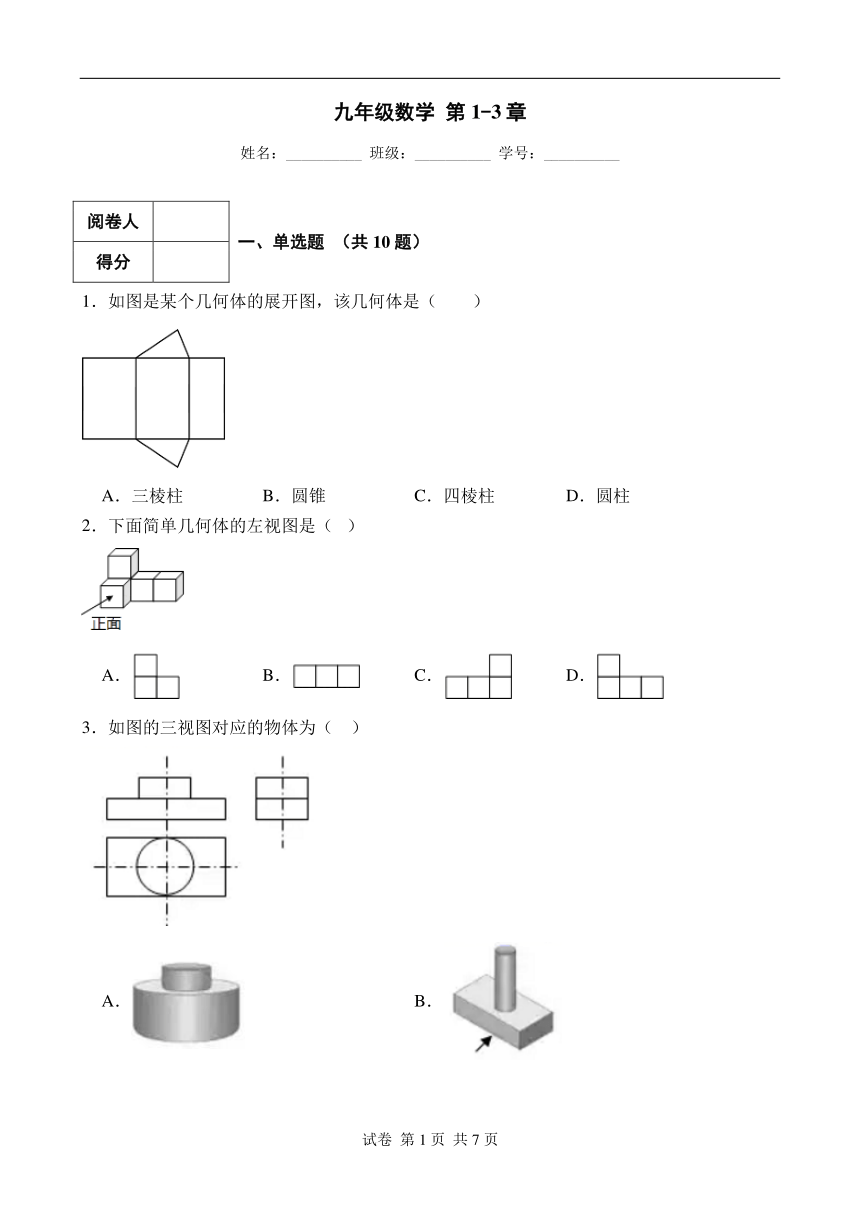
九年级数学 第1-3章 姓名:_____ 班级:_____ 学号:_____ 阅卷人 一、单选题 (共10题) 得分 1.如图是某个几何体的展开图,该几何体是( ) A.三棱柱 B.圆锥 C.四棱柱 D.圆柱 2.下面简单几何体的左视图是( ) A. B. C. D. 3.如图的三视图对应的物体为( ) A. B. C. D. 4.如图是由5个相同的小立方块组成的立体图形,则它的俯视图是( ) A. B. C. D. 5.如图是一个正方体的展开图,则在原正方体中,与“青”字相对的字是( ) A.共 B.建 C.绿 D.水 6.组成下列几何体的各面中,没有平面的是( ) A. B. C. D. 7.如图是由五个相同的小正方体搭成的一个几何体,它的主视图是( ) A. B. C. D. 8.由6个相同的小正方体搭成的几何体如图所示,则它从正面看到的视图是( ) A. B. C. D. 9.如图,现有一个圆心角为90°,半径为8cm的扇形纸片,用它恰好围成一个圆锥的侧面(接缝忽略不计),则该圆锥底面圆的半径为( ) A.4cm B.3cm C.2cm D.1cm 10.如图, 在中,,是的中点, 且,交于点,于点,连接.若,则的长是( ) A. B. C. D. 阅卷人 二、填空题 (共6题) 得分 11.点P是外一点,分别与相切于点A,B,连结,已知的半径为1,,则劣弧的长为 . 12.在中,,,则的值为 . 13.如图,在矩形ABCD中,AB=3,BC=4,P是对角线BD上的动点,以BP为直径作圆,当圆与矩形ABCD的边相切时,BP的长为 . 14.如图是某些几何体的表面展开图,则这些几何体分别是图1: ,图2: ,图3: . 15.如图,在矩形中,以点为圆心,长为半径画弧,交于点,交 于点.若,则阴影部分的面积为 . 16.若圆锥的母线长为6cm,侧面展开图的面积为,则底面半径是 cm. 阅卷人 三、计算题 (共1题) 得分 17.计算:. 阅卷人 四、解答题 (共7题) 得分 18.如图是由9个相同的小立方块搭成的几何体,请画出它的三视图. 19.在学习解直角三角形以后,某班数学兴趣小组的同学测量了旗杆的高度,如图,某一时刻,旗杆的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长为6米,落在斜坡上的影长为4米,,点、、三点共线,且,同一时刻,光线与旗杆的夹角为,斜坡的坡比为, (1)求坡角的度数; (2)旗杆的高度为多少米?(结果保留根号) 20.如图,在中,于D,,,,求的值. 21.2023年2月13日,21世纪以来第20个指导“三农”工作的中央一号文件《中共中央国务院关于做好2023年全面推进乡村振兴重点工作的意见》发布,体现了国家对“三农”的重视.实际上在古代,智慧的劳动人民有很多发明创造.如图即为古代劳动人民发明的“石磨”,其原理为在磨盘的边缘连接一个固定长度的“连杆”,推动“连杆”带动磨盘转动将粮食磨碎,物理学上称这种动力传输工具为“曲柄连杆机构”.小明受“石磨”的启发设计了一个“双连杆机构”,设计图如图1,两个固定长度的“连杆”,的连接点P在上,当点P在上转动时,带动点A,B分别在射线,上滑动,.如图2,当AP与相切时,点B恰好落在上.请就图2的情形解答下列问题: (1)若,求的度数. (2)若线段与交于点C,,,求的半径. 22.如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数(a≠0)的图象交于A、B两点,与x轴交于点C,过点A作ADy轴于点D,点O是线段CD的中点,AC=,sin∠ACD=,点B的坐标为(m,-2) (1)求反比例函数和一次函数的函数表达式; (2)求△ABD的面积. (3)观察图象,直接写出关于的不等式>的解集. 23.某市商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式自动扶梯 长为 ,坡角 为30°;改造后的斜坡式自动扶梯的坡角 为15°,改造后的斜坡式 ... ...
~~ 您好,已阅读到文档的结尾了 ~~