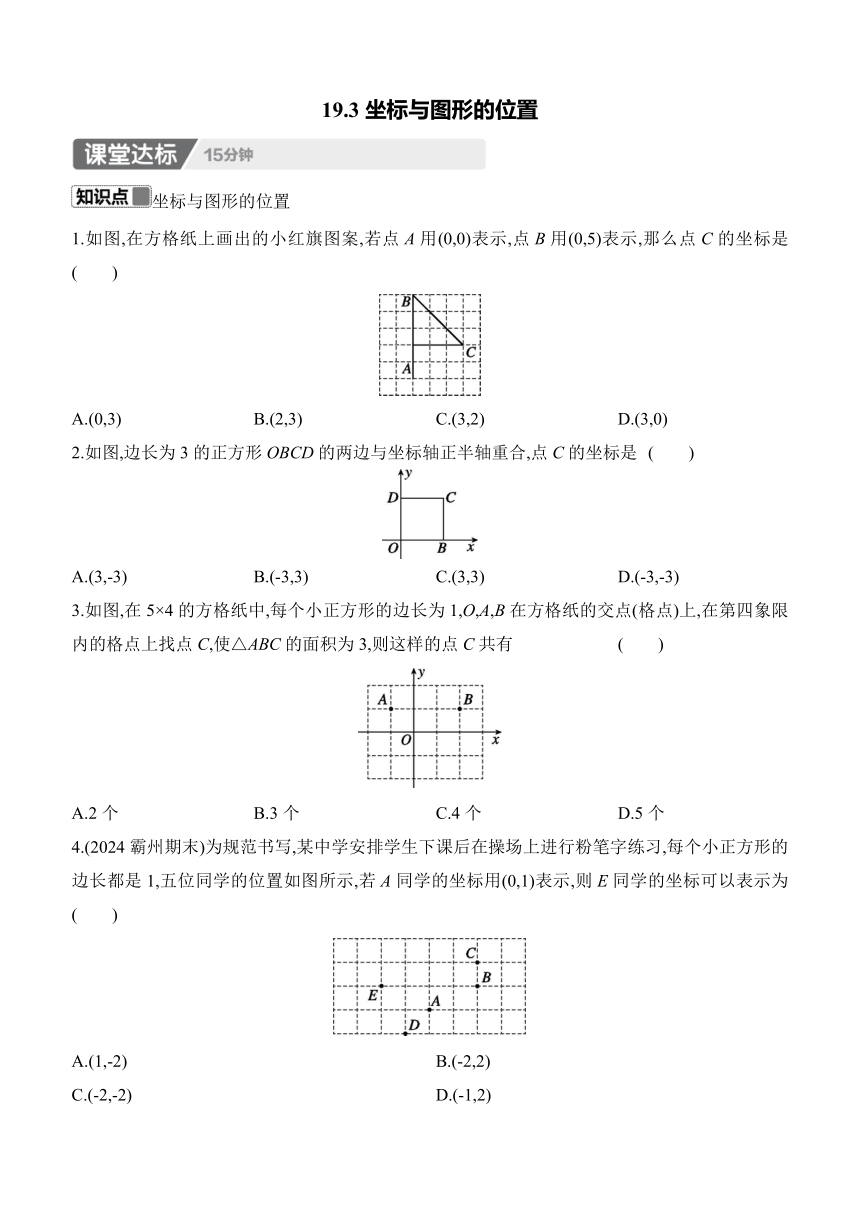
19.3 坐标与图形的位置 同步练（含答案）2024-2025学年数学冀教版八年级下册

19.3坐标与图形的位置 坐标与图形的位置 1.如图,在方格纸上画出的小红旗图案,若点A用(0,0)表示,点B用(0,5)表示,那么点C的坐标是 (　　) A.(0,3) B.(2,3) C.(3,2) D.(3,0) 2.如图,边长为3的正方形OBCD的两边与坐标轴正半轴重合,点C的坐标是 (　　) A.(3,-3) B.(-3,3) C.(3,3) D.(-3,-3) 3.如图,在5×4的方格纸中,每个小正方形的边长为1,O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使△ABC的面积为3,则这样的点C共有 (　　) A.2个 B.3个 C.4个 D.5个 4.(2024霸州期末)为规范书写,某中学安排学生下课后在操场上进行粉笔字练习,每个小正方形的边长都是1,五位同学的位置如图所示,若A同学的坐标用(0,1)表示,则E同学的坐标可以表示为 (　　) A.(1,-2) B.(-2,2) C.(-2,-2) D.(-1,2) 5.(2024贵州中考)为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中.若建立平面直角坐标系,使“创”“新”的坐标分别为 (-2,0),(0,0),则“技”所在的象限为 (　　) A.第一象限 B.第二象限 C.第三象限 D.第四象限 6.(2024唐山路北区期中)如图是阶梯的横截面(各拐角均为90°),每个台阶的高、宽分别是1和2,已知A,B,C,D,E为台阶拐角的顶点. (1)若以C为原点,在图中补画出x轴、y轴,并直接写出点A,D的坐标. (2)若以已知的5个台阶拐角顶点为原点,使其中的3个顶点落在第一象限,直接写出符合原点的位置. 1.如图是画在方格纸上的温州部分旅游景点简图,建立直角坐标系后,狮子岩、永嘉书院与埭头古村的坐标分别是(3,2),(-1,-3),(-3,0),则下列地点中离原点最近的是(　　) A.狮子岩 B.龙瀑仙洞 C.埭头古村 D.永嘉书院 2.(2024邢台月考)如图,某同学要从学校回家,所有道路的方向是向西或向北,若他的路线是(4,0)→(4,1)→■→(1,4)→(0,4),则阴影部分覆盖的数对可以是 (　　) A.(1,1) B.(3,2) C.(2,3) D.(4,3) 3.(2024唐山滦南县期末)如图,在平面直角坐标系中,有一只蜗牛从点A(2,3)的位置沿着射线AO的方向爬行到另一象限的点M,恰好OM=OA,则点M的坐标为 (　　) A.(-2,3) B.(-2,-3) C.(3,1) D.(2,-3) 4.如图,△ABC为等边三角形,B在坐标原点,点C的坐标为(4,0),则点A的坐标为　　　　. 5.如图,草房地基AB的长为15 m,房檐CD的长为20 m,门EF宽6 m,CD到地面的距离为18 m.请你建立适当的直角坐标系,并写出A,B,C,D,E,F的坐标. 6.(几何直观)已知点A(0,1),B(2,0),C(4,3). (1)在直角坐标系中描出各点,画出△ABC. (2)求△ABC的面积. (3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标. 【详解答案】 课堂达标 1.C　2.C　3.B　4.B　5.A 6.解:(1)建立平面直角坐标系,如图所示,A(-4,-2),D(2,1). (2)原点的位置是点B处. 课后提升 1.B　解析:如图,点O到狮子岩的距离为,点O到龙瀑仙洞的距离为2,点O到埭头古村的距离为3,点O到永嘉书院的距离为.∵2<3<,∴点O到龙瀑仙洞的距离最近.故选B. 2.A　解析:∵所有道路的方向是向西或向北,∴该同学的路线是(4,0)→(4,1)→(1,1)→(1,4)→(0,4).故选A. 3.B　解析:∵A(2,3),OM=OA且点M在射线AO上,∴点M与点A关于原点对称.∴点M的坐标为(-2,-3).故选B. 4.(2,2)　解析:如图,过点A作AD⊥BC于点D.∵△ABC为等边三角形,∴BD=CD=2,OA=4.根据勾股定理,得AD=2,∴点A的坐标为(2,2). 5.解:如图,以直线AB为x轴,以线段AB的中垂线为y轴,建立直角坐标系,则A(-7.5,0),B(7.5,0),E(-3,0),F(3,0), C(-10,18),D(10,18).(答案不唯一) 6.解:(1)如图所示: (2)如图,过点C分别向x,y轴作垂线,垂足分别为D,E. ∴四边形DOEC的面积=3×4=12,△BCD的面积=×2×3=3,△ACE的面积=×2×4=4,△AOB的面积=×2×1=1. ∴△ABC的面积=四边形DOEC的面积-△ACE的面积-△BCD的面积-△AOB的面积=12-4-3-1=4. ( ... ...