2025年寒假知识巩固第13章构造等腰三角形及最短路径问题练习题（含解析）

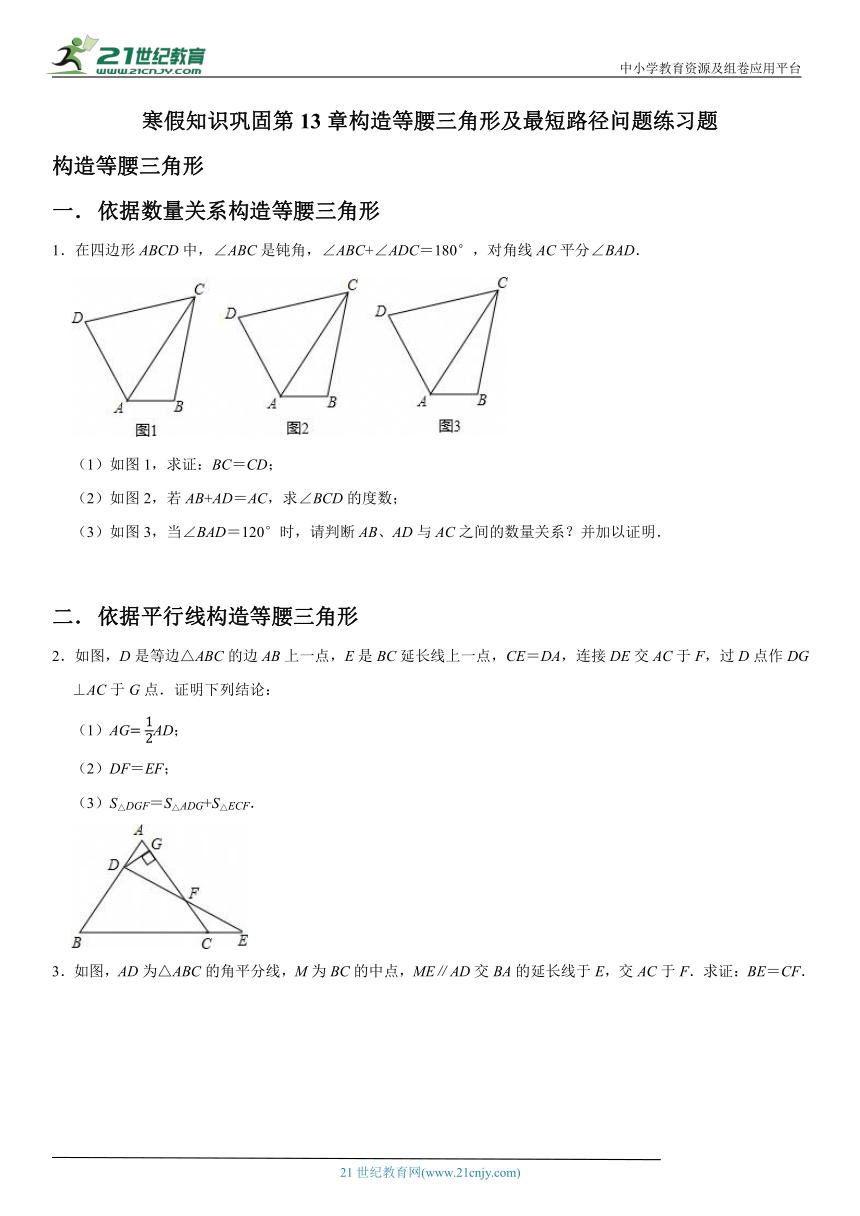
中小学教育资源及组卷应用平台 寒假知识巩固第13章构造等腰三角形及最短路径问题练习题 构造等腰三角形 依据数量关系构造等腰三角形 1．在四边形ABCD中，∠ABC是钝角，∠ABC+∠ADC＝180°，对角线AC平分∠BAD． （1）如图1，求证：BC＝CD； （2）如图2，若AB+AD＝AC，求∠BCD的度数； （3）如图3，当∠BAD＝120°时，请判断AB、AD与AC之间的数量关系？并加以证明． 依据平行线构造等腰三角形 2．如图，D是等边△ABC的边AB上一点，E是BC延长线上一点，CE＝DA，连接DE交AC于F，过D点作DG⊥AC于G点．证明下列结论： （1）AGAD； （2）DF＝EF； （3）S△DGF＝S△ADG+S△ECF． 3．如图，AD为△ABC的角平分线，M为BC的中点，ME∥AD交BA的延长线于E，交AC于F．求证：BE＝CF． 依据角平分线和垂线构造等腰三角形 4．如图，在△ABC中，BE平分∠ABC，AE⊥BE于点E，△BCE的面积为2，则△ABC的面积是 　 　． 5．情景观察： 如图1，△ABC中，AB＝AC，∠BAC＝45°，CD⊥AB，AE⊥BC，垂足分别为D，E，CD与AE交于点F． （1）写出图1中所有的全等三角形 　 　； （2）线段AF与线段CE的数量关系是AF＝2CE，并写出证明过程； 问题探究： 如图2，在△ABC中，∠BAC＝45°，AB＝BC，AD平分∠BAC，AD⊥CD，垂足为D，AD与BC交于点E．求证：AE＝2CD． 依据倍角关系构造等腰三角形 6．徐老师给爱好学习的小敏和小捷提出这样一个问题：如图1，△ABC中，∠B＝2∠C，AD是∠BAC的平分线．求证：AB+BD＝AC 小敏的证明思路是：在AC上截取AE＝AB，连接DE．（如图2） 小捷的证明思路是：延长CB至点E，使BE＝AB，连接AE．可以证得：AE＝DE（如图3）请你任意选择一种思路继续完成下一步的证明． 最短路径问题 两定一动型 7．如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，EF垂直平分BC，点P为直线EF上任意一点，则AP+BP的最小值是 　 　． 8．如图，在△ABC中，AB＝AC，BC＝4，△ABC的面积为12，AB的垂直平分线EF交AC于点F，若D为BC边的中点，M为线段EF上的一动点，求△BDM周长的最小值． 一定两动型 9．如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，AB＝5，AD平分∠CAB交BC于D点，E、F分别是AD，AC上的动点，则CE+EF的最小值为（　　） A． B．5 C．3 D． 10．如图，∠AOB＝30°，点P是∠AOB内一点，PO＝8，在∠AOB的两边上分别有点R、Q均不同于O）． （1）求△PQR周长的最小值； （2）当△PQR周长取最小值时，求∠QPR的值． 两定两动型 11．如图，在∠AOB内部有两点M、N，是在OA、OB上分别存在点E、F，使得E、F、M、N，四点组成的四边形的周长最短，找出E、F两点，并说明理由． 12．如图，∠AOB＝20°，点M，N分别是边OA，OB上的定点，点P，Q分别是边OB、OA上的动点． （1）画图说明，当MP+PQ+QN最小时，找出P和Q的位置． （2）记∠MPQ＝α，∠PQN＝β，当MP+PQ+QN最小时，求β﹣α的值． 参考答案 1．解（1）如图1，过点C作CM⊥AB，交AB的延长线于点M；作CN⊥AD，垂足为N； ∵AC平分∠DAB，∴CM＝CN； 又∵∠ABC+∠ADC＝180°，∠MBC+∠ABC＝180°； ∴∠NDC＝∠MBC， 在△NDC与△MBC中，∵； ∴BC＝DC； （2）如图2，延长AB到E，使BE＝AD； ∵AB+AD＝AC，∴AE＝AC； 由（1）知∠ADC＝∠EBC；在△ADC与△EBC中， ∵，∴△ADC≌△EBC，故AC＝EC； 又∵AE＝AC，∴AE＝AC＝EC， 故△AEC为等边三角形，∠CAB＝60°； ∴∠BAD＝120°，∠BCD＝360°﹣180°﹣120°＝60°， 即∠BCD＝60°． （3）若AB＝AD；在△ADC与△ABC中， ∵，∴△ADC≌△ABC， ∴∠ADC＝∠ABC， 故∠DCA＝90°﹣60°＝30°， ∴AC＝2AD；而AD+AB＝2AD， ∴AC＝AD+AB； 若AD＞AB；如图2，延长AB到E，使BE＝AD； 由（2）可知△ADC≌△EBC， ∴∠E＝∠DAC＝60°；而∠CAB＝60°， ∴△CAE是等边 ... ...