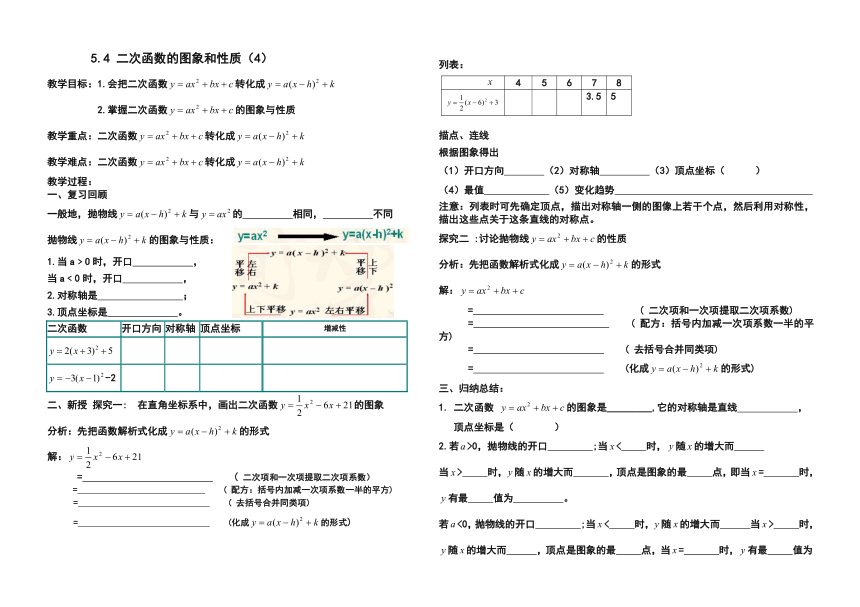
5.4 二次函数的图象和性质(4) 教学目标:1.会把二次函数转化成 2.掌握二次函数的图象与性质 教学重点:二次函数转化成 教学难点:二次函数转化成 教学过程: 一、复习回顾 一般地,抛物线与的 相同, 不同 抛物线的图象与性质: 1.当a﹥0时,开口 , 当a﹤0时,开口 , 2.对称轴是 ; 3.顶点坐标是 。 二次函数 开口方向 对称轴 顶点坐标 增减性 -2 二、新授 探究一: 在直角坐标系中,画出二次函数的图象 分析:先把函数解析式化成的形式 解: = ( 二次项和一次项提取二次项系数) = ( 配方:括号内加减一次项系数一半的平方) = ( 去括号合并同类项) = (化成的形式) 列表: 4 5 6 7 8 3.5 5 描点、连线 根据图象得出 (1)开口方向 (2)对称轴 (3)顶点坐标( ) (4)最值 (5)变化趋势 注意:列表时可先确定顶点,描出对称轴一侧的图像上若干个点,然后利用对称性,描出这些点关于这条直线的对称点。 探究二 :讨论抛物线的性质 分析:先把函数解析式化成的形式 解: = ( 二次项和一次项提取二次项系数) = ( 配方:括号内加减一次项系数一半的平方) = ( 去括号合并同类项) = (化成的形式) 三、归纳总结: 二次函数 的图象是_____,它的对称轴是直线 , 顶点坐标是( ) 2.若>0,抛物线的开口 ;当< 时,随的增大而 当> 时,随的增大而 ,顶点是图象的最 点,即当= 时,有最 值为 。 若<0,抛物线的开口 ;当< 时,随的增大而 当> 时,随的增大而 ,顶点是图象的最 点,当= 时,有最 值为 3.求出下列抛物线对称轴及顶点坐标,并说出它的开口方向,最值,增减性。 课下作业: 1.(1)抛物线与轴的交点坐标是 (2)抛物线的一段如图所示, 则这条抛物线的对称轴是 它可以由抛物线向 平移 单位长度, 再向 平移 单位长度而得到 2.如果,那么抛物线的顶点在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.已知,那么抛物线的图象大致是( ) 5.已知抛物线,其中。回答下列问题,并说明理由: (1)抛物线与轴的交点在轴的正半轴上还是在轴的负半轴上? (2)抛物线的对称轴在轴的左侧还是右侧? (3)抛物线的顶点在哪一象限或哪条坐标轴上? 6.如果将抛物线沿直角坐标平面向左平移2个单位长度,在向上平移3个单位长度得到抛物线抛物线,则b= c= 8.(选做)如图,已知抛物线y= x2+mx+3与x轴交于A,B两点,与y轴交于点C,点B的坐标为(3,0) (1)求m的值及抛物线的顶点坐标。 (2)点P是抛物线对称轴l上的一个动点,当PA+PC的值最小时,求点P的坐标。
~~ 您好,已阅读到文档的结尾了 ~~