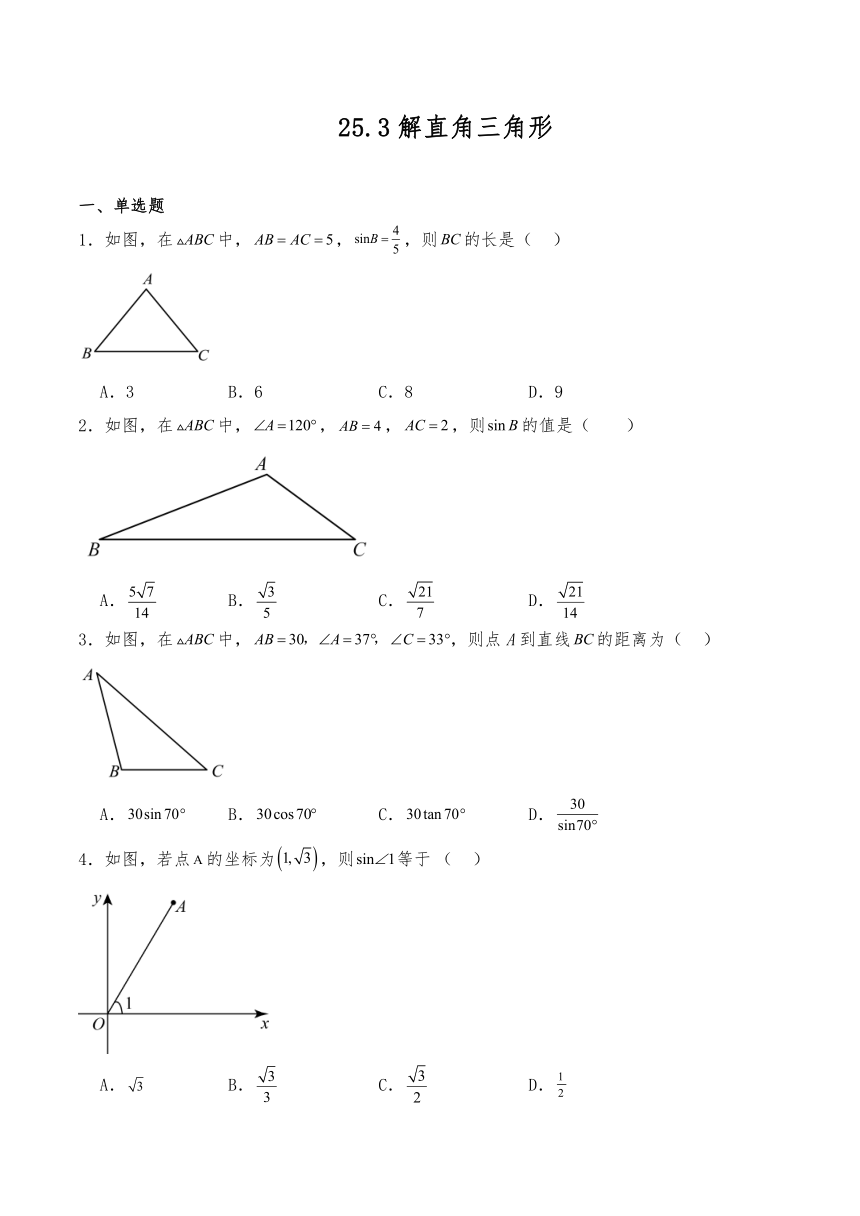
25.3解直角三角形 一、单选题 1.如图,在中,,,则的长是( ) A.3 B.6 C.8 D.9 2.如图,在中,,,,则的值是( ) A. B. C. D. 3.如图,在中,,则点A到直线的距离为( ) A. B. C. D. 4.如图,若点的坐标为,则等于( ) A. B. C. D. 5.在边长相等的小正方形组成的网格中,点,,都在格点上,那么的值为( ) A. B. C. D. 6.在四边形中,,,,,,则四边形周长为( ) A. B. C. D. 7.如图,在中,和都是锐角,若,,则( ) A. B. C. D. 8.如图,直线与坐标轴交于点A、,过点作的垂线交轴于点,则点的坐标为( ) A. B. C. D. 9.如图,在平面直角坐标系中,矩形的顶点A在第一象限,B,D分别在y轴上,O是的中点.若,则点C的坐标是( ) A.(3,) B. C.,3) D. 10.如图,正方形的边长为,为上一点,连接,于点,连接,若,则的面积为( ) A.5 B.6 C.7 D.8 二、填空题 11.如图,已知△ABC中,,,则AC= cm. 12.如图,在中,,,,则的长为 . 13.如图,在四边形ABCD中,∠B=∠D=90°,AB=3, BC=2,tanA=,则CD= . 14.如图3,在中,,是边的中点,过作,垂足为点,如果,,那么 . 15.如图:两张宽度都为的纸条交叉重叠在一起,两张纸条交叉的夹角为α(见图中的标注),则重叠(阴影)部分的面积表示为 . 16.如图,在中,,为上一点,,,.则= . 17.如果一个四边形的某个顶点到其他三个顶点的距离相等,我们把这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.如图,已知梯形ABCD是等距四边形,AB∥CD,点B是等距点.若BC=10,cosA=,则CD的长等于 . 18.如图,在中,,点在边上,点在射线上,将沿翻折,使得点落在点处,当且时,的长为 . 三、解答题 19.如图所示,在中,,是边上的中线,过点D作,垂足为E,若. (1)求的长; (2)求的正切值. 20.如图,在中,,,,点在边上,且,,垂足为,联结. (1)求线段的长; (2)求的正切值. 21.如图,在中,,,点在边AC上,且,,垂足为点,联结,求: (1)线段的长; (2)的余弦值. 22.如图,在中,是边上的高.已知,,. (1)求的长; (2)如果点E是边的中点,连接,求的值. 23.已知:如图,第一象限内的点在反比例函数的图像上,点在轴上,轴,点的坐标为,且.求: (1)反比例函数的解析式; (2)点的坐标; (3)的余弦值. 24.在中,,,点为线段上一动点,连接. (1)如图1,若,,求线段的长. (2)如图2,以为边在上方作等边,点是的中点,连接并延长,交的延长线于点. 若,求证:. 25.如图,在矩形中,,是边上一动点,是线段延长线上一点,且,与矩形对角线交于点. (1)当点与点重合时,如果,求的长; (2)当点在线段的延长线上, ①求的值; ②如果,求的余切值. 答案 一、单选题 1.B 【分析】本题考查解直角三角形,等腰三角形的性质,勾股定理.正确作出辅助线是解题关键.过点A作于点D.由等腰三角形三线合一的性质得出.根据,可求出,最后根据勾股定理可求出,即得出. 【解析】解:如图,过点A作于点D. ∵, ∴. 在中,, ∴, ∴, ∴. 故选B. 2.D 【分析】本题主要考查解直角三角形,过点C作,交的延长线于点D,在中,可求得和,利用勾股定理求得,根据正弦定义即可求得答案. 【解析】解:过点C作,交的延长线于点D, ∵, ∴, 在中,, ∴, , ∵, ∴, 在中,, ∴. 故选:D. 3.A 【分析】根据题意为求点A到直线的距离,即求中边上的高,构造直角三角形,利用已知信息结合三角函数的定义解之即可.本题考查了解直角三角形 构造直角三角形,熟练掌握解直角三角形是解题的关键. 【解析】解:依题意,过点A作,交延长线于点D, ∵, ∴, 在中 ... ...
~~ 您好,已阅读到文档的结尾了 ~~

