专题五四边形——2025届中考数学二轮专题达标训练（含解析）

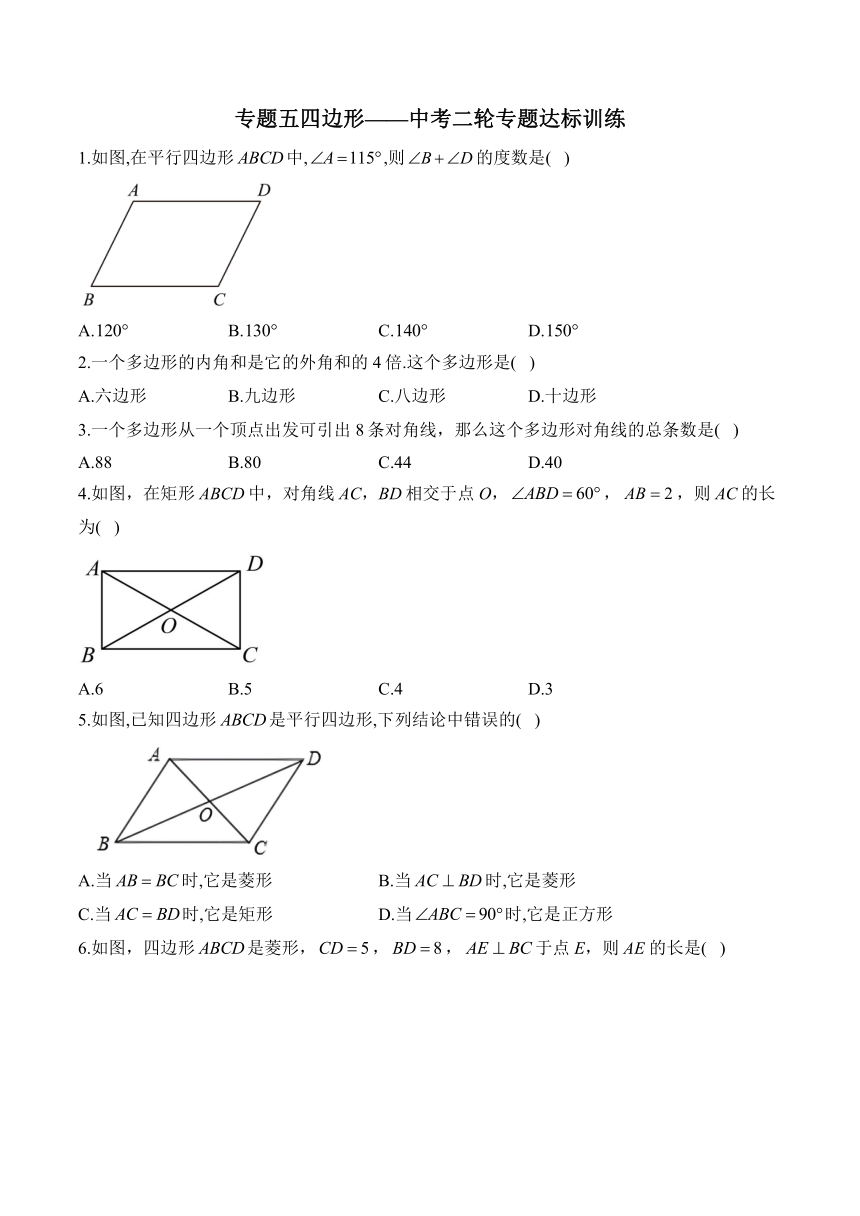
专题五四边形———中考二轮专题达标训练 1.如图,在平行四边形中,,则的度数是( ) A. B. C. D. 2.一个多边形的内角和是它的外角和的4倍.这个多边形是( ) A.六边形 B.九边形 C.八边形 D.十边形 3.一个多边形从一个顶点出发可引出8条对角线，那么这个多边形对角线的总条数是( ) A.88 B.80 C.44 D.40 4.如图，在矩形ABCD中，对角线AC，BD相交于点O，，，则AC的长为( ) A.6 B.5 C.4 D.3 5.如图,已知四边形是平行四边形,下列结论中错误的( ) A.当时,它是菱形 B.当时,它是菱形 C.当时,它是矩形 D.当时,它是正方形 6.如图，四边形是菱形，，，于点E，则的长是( ) A. B.6 C. D. 7.如图,的对角线,相交于点O,的平分线与边相交于点P,E是的中点,若,,则的长为( ) A.1 B. C. D.2 8.如图,菱形的对角线,相交于点O,过点C作,交于点E,连接,若,,则的长为( ) A. B. C. D. 9.如图,在平面直角坐标系中,长方形的顶点A,C的坐标分别是,,点B在x轴上,则点B的横坐标是( ) A.4 B. C. D.5 10.如图,在正方形中,点E是上一点,延长至点F,使,连结,,,交于点K,过点A作,垂足为点H,交于点G,连结,.下列四个结论：①；②；③；④.其中正确结论的个数为( ) A.1个 B.2个 C.3个 D.4个 11.如图,,则_____度. 12.已知正方形边长为2,E是边上一点,将此正方形的一个角沿直线折叠,使C点恰好落在对角线上,则的长等于_____. 13.如图,在平行四边形中,E是线段上一点,连结、交于点F.若,则_____. 14.如图,菱形的对角线、交于点O,过点O作,且,连接、.若,,则_____度,的长为_____. 15.如图，矩形ABCD的对角线AC，BD相交于点O，延长BC至点G，连接DG，，点E为DG的中点，连接OE交CD于点F，若，，则DF的长为_____. 16.如图,菱形的对角线、相交于点O,,,与交于点F. (1)求证：四边形为矩形； (2)若,,求菱形的面积. 17.如图,平行四边形的对角线、相交于点O,平分,过点D作,过点C作,、交于点P,连接. (1)求证：四边形是菱形； (2)若,,求的长. 18.在中，过点D作于点E，点F在上，，连接、. （1）求证：四边形是矩形； （2）若平分，，.求的长. 19.如图，已知正方形中，E为上一点.将正方形折叠起来使点A和点E重合，折痕为.若，. (1)求的长； (2)求的面积. 20.（1）如图1，在矩形ABCD中，点E，F分别在边DC，BC上，，垂足为点G.求证：. 【问题解决】 （2）如图2，在正方形ABCD中，点E，F分别在边DC，BC上，，延长BC到点H，使，连接DH.求证：. 【类比迁移】 （3）如图3，在菱形ABCD中，点E，F分别在边DC，BC上，，，，求CF的长. 答案以及解析 1.答案：B 解析：∵四边形是平行四边形, ∴,, ∴, 又∵, ∴, ∴, 故选：B. 2.答案：D 解析：多边形外角和是,设多边形边数为n, 故多边形的内角和为, 解得, 故选D. 3.答案：C 解析：设这个多边形的边数为n， 一个多边形从一个顶点出发共引8条对角线， ， 解得：， 总的对角线的条数为：（条）. 故选：C. 4.答案：C 解析：四边形为矩形, . 又,是等边三角形, , . 故选C. 5.答案：D 解析：A、四边形ABCD是平行四边形, 又 四边形ABCD是矩形,故本选项不符合题意; B、四边形ABCD是平行四边形, 又, 四边形ABCD是菱形,故本选项不符合题意; C、四边形ABCD是平行四边形, 又, 四边形ABCD是菱形,故本选项不符合题意; D、四边形ABCD是平行四边形, 又, 四边形ABCD是矩形,不一定是正方形,故本选项符合题意; 故选:D. 6.答案：A 解析：四边形是菱形，，， ，，， 在中，， ， 菱形的面积为， ， 故选：A. 7.答案：A 解析：在中,,,, ； 平分, , , ； ； E是的中点,, ； 故选：A. 8.答案：D 解析：∵四边形是菱形, ∴,. 在中,是斜边上的中线, ∴, ∴. 在中,. ∴, 即, 解得. 故选：D. 9.答案：D 解析：过点A、C作轴,轴于点E、D,如图： , ∴, ∵点A的坐标是,点C的坐标是 ∴,, ∵四边形是矩形, ∴, ... ...