专题七图形的变化——2025届中考数学二轮专题达标训练（含解析）

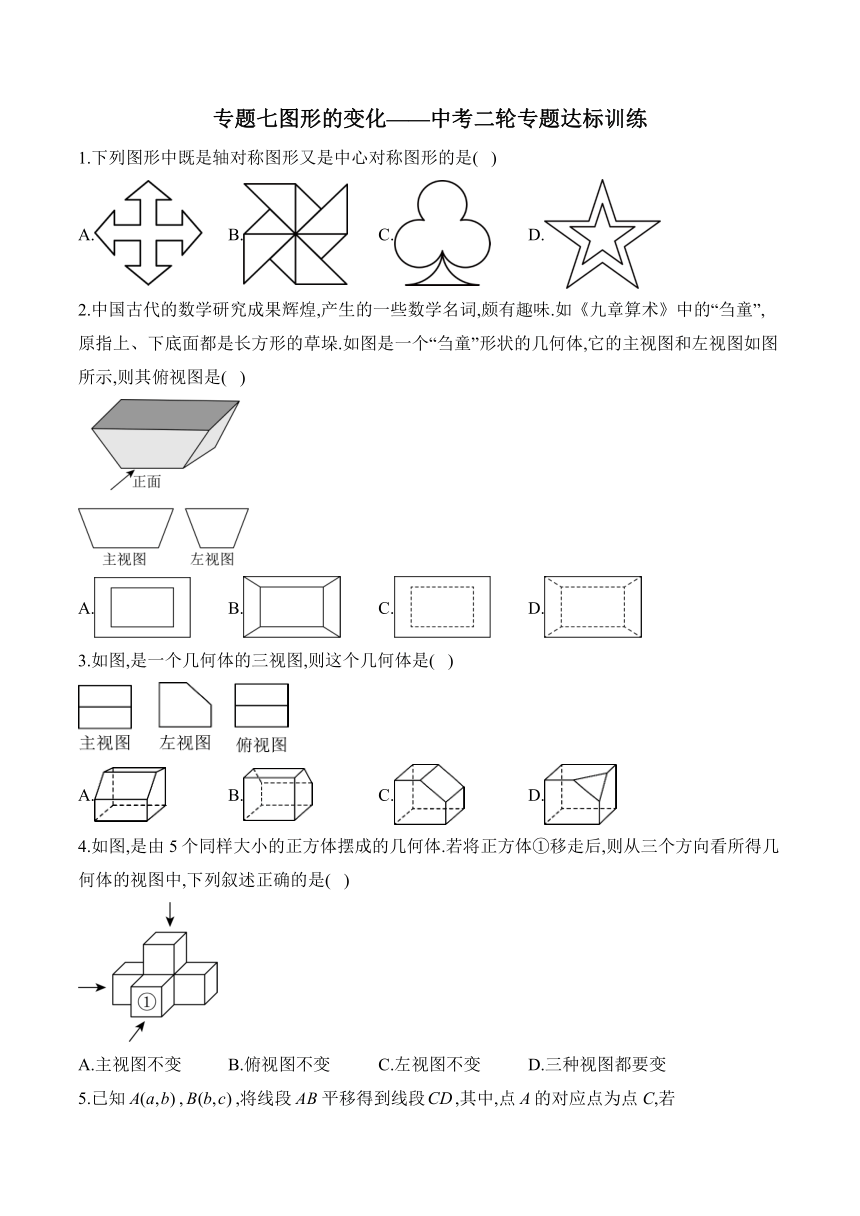
专题七图形的变化———中考二轮专题达标训练 1.下列图形中既是轴对称图形又是中心对称图形的是( ) A. B. C. D. 2.中国古代的数学研究成果辉煌,产生的一些数学名词,颇有趣味.如《九章算术》中的“刍童”,原指上、下底面都是长方形的草垛.如图是一个“刍童”形状的几何体,它的主视图和左视图如图所示,则其俯视图是( ) A. B. C. D. 3.如图,是一个几何体的三视图,则这个几何体是( ) A. B. C. D. 4.如图,是由5个同样大小的正方体摆成的几何体.若将正方体①移走后,则从三个方向看所得几何体的视图中,下列叙述正确的是( ) A.主视图不变 B.俯视图不变 C.左视图不变 D.三种视图都要变 5.已知,,将线段平移得到线段,其中,点A的对应点为点C,若,,则的值为( ) A. B.1 C. D.5 6.如图,在中,,将绕点A逆时针旋转,得到,连接.若,,则线段的长为( ) A. B. C. D. 7.如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,将绕着点A顺时针旋转,得到,则点C的坐标是( ) A. B. C. D. 8.已知锐角如图; (1)在射线OA上取一点C,以点O为圆心,OC长为半径作,交射线OB于点D,连接CD； (2)分别以点C,D为圆心,CD长为半径作弧,交于点M,N； (3)连接OM,MN. 根据以上作图过程及所作图形,下列结论中错误的是( ) A. B.若,则 C. D. 9.如图，已知，点M在边上，且，点N和点P分别是和上的一个动点，则的最小值为( ) A.1 B.2 C.3 D.4 10.如图,原点O为的对称中心,轴,与y轴交于点,与x轴交于,.若将绕原点O顺时针旋转,每次旋转,则第2024次旋转结束时,点A的对应点的坐标( ) A. B. C. D. 11.点关于原点的对称点是，则_____. 12.为了测得一棵树的高度，一个小组的同学进行了如下测量：在阳光下，测得一根与地面垂直、长为1米的竹竿的影长为米.同时发现这棵树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图），测得墙壁上的影长为米，落在地面上的影长为3米，则这棵树的高度为_____. 13.如图，在平面直角坐标系中，点A的坐标为，点B的坐标为，连接AB，若将绕点B顺时针旋转，得到，则点的坐标为____. 14.如图,在中,以点C为圆心,任意长为半径作弧,分别交,于点D,E；分别以点D,E为圆心,大于的长为半径作弧,两弧交于点F；作射线交于点G,若,,的面积为8,则的面积为_____. 15.如图，在平面直角坐标系中，已知，，过点B作y轴的垂线l，P为直线l上一动点，连接，，则的最小值为_____. 16.如图,,,,将向右平移3个单位长度,然后再向上平移1个单位长度,可以得到. (1)画出平移后的,并写出,,的坐标； (2)画出绕点C顺时针旋转后得到的,并写出点的坐标： (3)在x轴上存在点P,使得面积为,直接写出点P的坐标. 17.如图,已知矩形,,. (1)作的角平分线分别交于点E,对角线于点F(要求：尺规作图保留作图痕迹,不写作法.标明字母)； (2)求的长. 18.如图,等腰直角中,,点P在上,将绕顶点B沿顺时针方向旋转后得到. (1)求的度数； (2)若,,求的长. 19.如图,在中,,点D,E在上,,连接,. (1)请画出线段,使得与关于直线对称. (2)在(1)的条件下,连接,判断的形状,并说明理由. 20.综合实践 问题背景：借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究.如图1,在“中,,,分别取,的中点D,E,作.如图2所示,将绕点A逆时针旋转,连接,. (1)探究发现：旋转过程中,线段和的长度存在怎样的数量关系？写出你的猜想,并证明. (2)性质应用：如图3,当所在直线首次经过点B时,求的长. (3)延伸思考：如图4,在中,,,,分别取,的中点D,E.作,将绕点B逆时针旋转,连接,.当边平分线段时,求的值. 答案以及解析 1.答案：A 解析：A、该图形既是轴对称图形,也是中心对称图形,故A符合题意； B、该图形不是轴对称图形,是中心对称图形,故B不符合题意； C、该图形是轴对称图形 ... ...